Page 21 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Oscillatory Motion Chap. 1

ib)
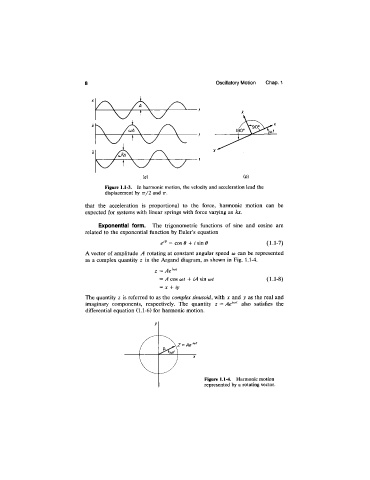
Figure 1.1-3. In harmonic motion, the velocity and acceleration lead the
displacement by tt/ 2 and tt.

that the acceleration is proportional to the force, harmonic motion can be
expected for systems with linear springs with force varying as kx.

Exponential form. The trigonometric functions of sine and cosine are
related to the exponential function by Euler’s equation
= cos 8 + i sin 8
A vector of amplitude A rotating at constant angular speed u) can be represented
as a complex quantity z in the Argand diagram, as shown in Fig. 1.1-4.

z =
= A cos o)t -V iA sin o)t ( 1.1-8)
= jc + /y
The quantity z is referred to as the complex sinusoid, with x and y as the real and
imaginary components, respectively. The quantity z = Ae^"^^ also satisfies the
differential equation (1.1-6) for harmonic motion.

Figure 1.1-4. Harmonic motion
represented by a rotating vector.