Page 23 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Oscillatory Motion Chap. 1
10

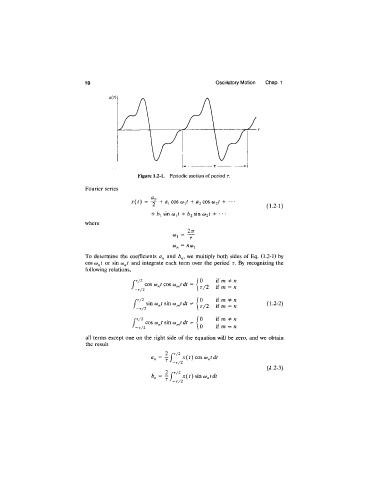
Figure 1.2-1. Periodic motion of period r.
Fourier series

x(i) = ^ + cos (O^t + «2 ^ 2^ + • • *
( 1.2-1)
+ fcj sin (x)^t + ¿>2 ^ 2^ + • • •
where
277
0)i = ----
^ T

To determine the coefficients and we multiply both sides of Eq. (1.2-1) by
cos (oj or sin coj and integrate each term over the period r. By recognizing the
following relations,
/ 1 _ / 0 ii m n
fr/2
COS 0)J cos (X),
^ \ if m = A7
- r / 2
■/2 _ i 0 if m n
f sm (o„t sm 0), ^ I r/2 if m = A 2 (1.2-2)
- r/2
t/2
rr/l . I O 0 if m ^ n
/ COS (o^t sm co^tdt = <
•'-r/2 10 if m = n
all terms except one on the right side of the equation will be zero, and we obtain
the result
2 “^/^
a„ = - r x{t)cosco„tdt
^ •'-r/2
(.1.2-3)
2 /*r/2
= — r jc(i) sin iojdt
•'-r/2