Page 27 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Oscillatory Motion Chap. 1
14

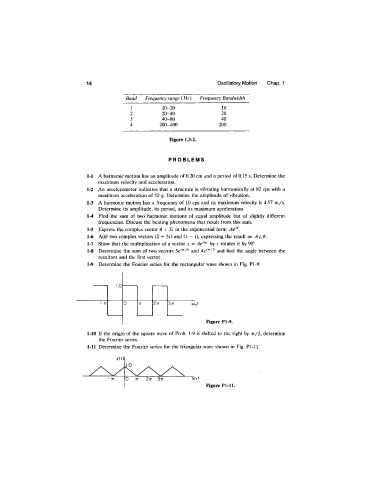
Band Frequency range (Hz) Frequency Bandwidth
1 10-20 10
2 20-40 20
3 40-80 40
4 200-400 200

Figure 1.3-2.

PROBLEMS

1-1 A harmonic motion has an amplitude of 0.20 cm and a period of 0.15 s. Determine the
maximum velocity and acceleration.
1-2 An accelerometer indicates that a structure is vibrating harmonically at 82 cps with a
maximum acceleration of 50 g. Determine the amplitude of vibration.
1-3 A harmonic motion has a frequency of 10 cps and its maximum velocity is 4.57 m/s.
Determine its amplitude, its period, and its maximum acceleration.
1-4 Find the sum of two harmonic motions of equal amplitude but of slightly different
frequencies. Discuss the beating phenomena that result from this sum.
1-5 Express the complex vector 4 + 3/ in the exponential form Ae‘^.
1-6 Add two complex vectors (2 + 3/) and (4 - /), expressing the result as ALB.
1-7 Show that the multiplication of a vector z = by i rotates it by 90°.
1-8 Determine the sum of two vectors 5^'^^^ and and find the angle between the
resultant and the first vector.
1-9 Determine the Fourier series for the rectangular wave shown in Fig. PI-9.

Figure PI-9.
1-10 If the origin of the square wave of Prob. 1-9 is shifted to the right by 7t/2 , determine
the Fourier series.
1-11 Determine the Fourier series for the triangular wave shown in Fig. PI-11.

Figure Pl-11.