Page 246 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

Chap. 7 Problems 233

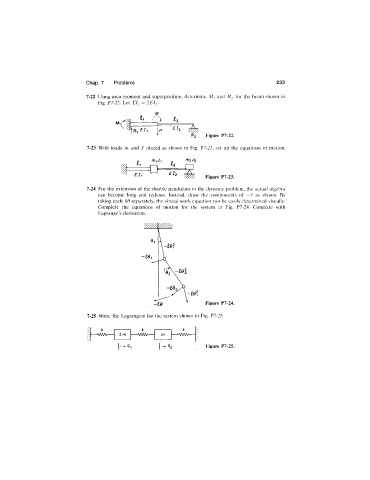
7-22 Using area moment and superposition, determine M, and /?2 for the beam shown in
Fig. P7-22. Let £/, = 2El,.
M
t,
"’Cf
EU El,
f f . Figure P7-22.
7-23 With loads m and J placed as shown in Fig. P7-23, set up the equations of motion.
/TI2 '^2 .
% 1 3
El, Eh Figure P7-23.
7-24 For the extension of the double pendulum to the dynamic problem, the actual algebra
can become long and tedious. Instead, draw the components of —r as shown. By
taking each 86 separately, the virtual work equation can be easily determined visually.
Complete the equations of motion for the system in Fig. P7-24. Compare with
Lagrange’s derivation.

Figure P7-24.

7-25 Write the Lagrangian for the system shown in Fig. P7-25

Figure P7-25.