Page 327 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

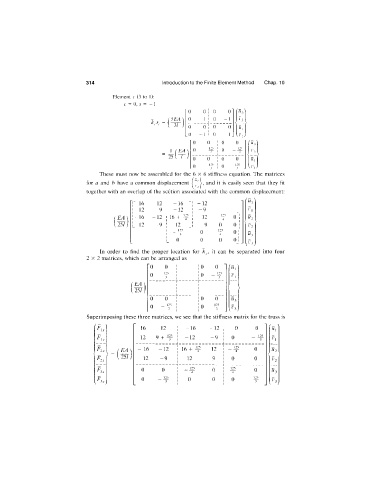
314 Introduction to the Finite Element Method Chap. 10

Element c (3 to 1):
c = 0,s = -1
"0 0 1 0 0
1

i SEA \ 0 1 1 0 -1 L'-
1

^ “ I 3/ ) 0 0 1 0 0
1 ^1
_0 -1 1 0 1J v r , ;
” 0 0 i 0 0
12S 1 125

_ 1 ( EA 0 ^ 1 0 3

~ 25 [ I J
0 0 1 0 0
125 1 125 1
_ 0 r 1 0 3 IrJ
These must now be assembled for the 6 x 6 stiffness equation. The matrices
for a and b have a common displacement is easily seen that they fit
together with an overlap of the section associated with the common displacement:
r 12 -1 6 ■] -1 2
1 12 9 -1 2 I - 9

EA |- 1 6 -1 2 ; 16 + ^ ; 12 125 0 2
4
251 !_- 12 - 9 ! 12 _l 9 0 0 2
1 125 125
1 4 0 4 0
1 0 0 0 0
In order to find the proper location for it can be separated into four
2 x 2 matrices, which can be arranged as
” 0 0 ! 1 0 0

125
0 ¥ i 1 0 3

1
T r
EA 1 1
<
25/ 1 1
4- u
0 0 1 1 0 0 ^3
125 1 125
0 1 0 3
“ “ 1 1
Superimposing these three matrices, we see that the stiffness matrix for the truss is
i E 16 12 1 -1 6 - 12 1 1 0 0 'u^
1
^Ix
1 1
12 9 + ^ 1 -1 2 - 9 1 1 0 125
3
1
. J_ .A
1 1 125
E - 16 -1 2 1 16 + 12 1 1 4 0 Ul
1
1 U s / j 1 1 <
K -1 2 - 9 1 12 9 1 1 0 0 V2
1

- H- 125 ■-1 -
1
1 125
E 0 0 1 4 0 1 1 4 0
1
125 1 1 125
0 3 1 0 0 1 0 3 ^3
1 1 1