Page 433 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

420 Random Vibrations Chap. 13

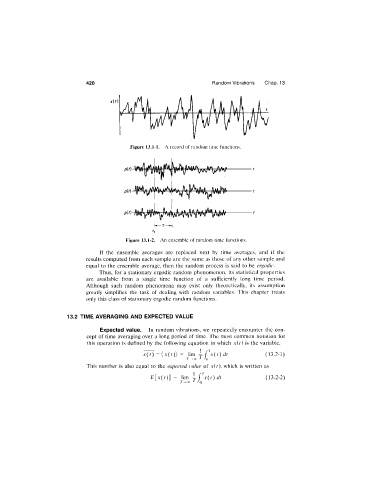
Figure 13.1-1. A record of random time functions.

p{f)-

pit)-

pit)-

U - .-

Figure 13.1-2. An ensemble of random time functions.

If the ensemble averages are replaced next by time averages, and if the
results computed from each sample are the same as those of any other sample and
equal to the ensemble average, then the random process is said to be ergodic.
Thus, for a stationary ergodic random phenomenon, its statistical properties
are available from a single time function of a sufficiently long time period.
Although such random phenomena may exist only theoretically, its assumption
greatly simplifies the task of dealing with random variables. This chapter treats
only this class of stationary ergodic random functions.

13.2 TIME AVERAGING AND EXPECTED VALUE

Expected value. In random vibrations, we repeatedly encounter the con­
cept of time averaging over a long period of time. The most common notation for
this operation is defined by the following equation in which x{t) is the variable.
x { t ) = { x { t ) ) = Wva ( x{t) dt (13.2-1)
7'_^oc ^0
This number is also equal to the expected value of x{t), which is written as
E[x{t)] = lim Y Í '^ (0 (13.2-2)
7 ' - > o c ^ ^0