Page 108 - Bird R.B. Transport phenomena

§3.6 Use of the Equations of Change to Solve Flow Problems 93

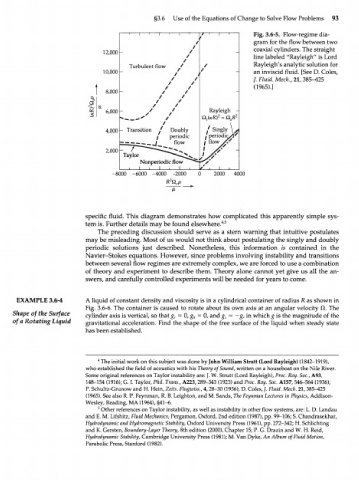
I ' I ' / ' Г Fig. 3.6-5. Flow-regime dia-
gram for the flow between two
coaxial cylinders. The straight
12,000
line labeled "Rayleigh" is Lord
Turbulent flow / Rayleigh's analytic solution for
10,000 / an inviscid fluid. [See D. Coles,
/. Fluid. Mech., 21,385-425
(1965).]
8,000
9.
сГ
6,000 Rayleigh -

4,000 Transition / Doubly ' Singly Ь
/ periodic I periodic/l^
2,000

-8000 -6000 -4000 -2000 2000 4000

specific fluid. This diagram demonstrates how complicated this apparently simple sys-
4 5
tem is. Further details may be found elsewhere. '
The preceding discussion should serve as a stern warning that intuitive postulates
may be misleading. Most of us would not think about postulating the singly and doubly
periodic solutions just described. Nonetheless, this information is contained in the
Navier-Stokes equations. However, since problems involving instability and transitions
between several flow regimes are extremely complex, we are forced to use a combination
of theory and experiment to describe them. Theory alone cannot yet give us all the an-
swers, and carefully controlled experiments will be needed for years to come.

EXAMPLE 3.6-4 A liquid of constant density and viscosity is in a cylindrical container of radius R as shown in
Fig. 3.6-6. The container is caused to rotate about its own axis at an angular velocity П. The
Shape of the Surface cylinder axis is vertical, so that g = 0, g = 0, and g = —g, in which g is the magnitude of the
z
r
0
of a Rotating Liquid gravitational acceleration. Find the shape of the free surface of the liquid when steady state
has been established.

4
The initial work on this subject was done by John William Strutt (Lord Rayleigh) (1842-1919),
who established the field of acoustics with his Theory of Sound, written on a houseboat on the Nile River.
Some original references on Taylor instability are: J. W. Strutt (Lord Rayleigh), Proc. Roy. Soc, A93,
148-154 (1916); G. I. Taylor, Phil. Trans., A223, 289-343 (1923) and Proc. Roy. Soc. A157, 546-564 (1936);
P. Schultz-Grunow and H. Hein, Zeits. Flugwiss., 4, 28-30 (1956); D. Coles, /. Fluid. Mech. 21, 385-425
(1965). See also R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures in Physics, Addison-
Wesley, Reading, MA (1964), §41-6.
0
Other references on Taylor instability, as well as instability in other flow systems, are: L. D. Landau
and E. M. Lifshitz, Fluid Mechanics, Pergamon, Oxford, 2nd edition (1987), pp. 99-106; S. Chandrasekhar,
Hydrodynamic and Hydromagnetic Stability, Oxford University Press (1961), pp. 272-342; H. Schlichting
and K. Gersten, Boundary-Layer Theory, 8th edition (2000), Chapter 15; P. G. Drazin and W. H. Reid,
Hydrodynamic Stability, Cambridge University Press (1981); M. Van Dyke, An Album of Fluid Motion,
Parabolic Press, Stanford (1982).