Page 138 - Bird R.B. Transport phenomena

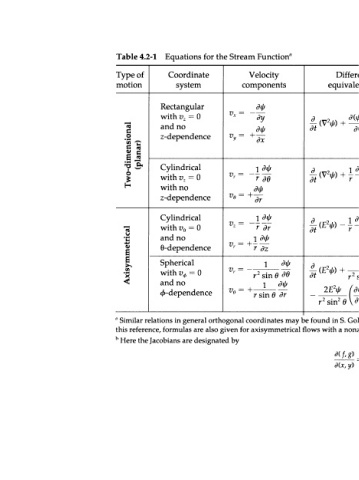
Table 4.2-1 Equations for the Stream Function"

Type of Coordinate Velocity Differential equations for ф which are Expressions for
motion system components equivalent to the Navier-Stokes equation* 7 operators

Rectangular <? 2 <? 2
with v = 0 Vx= дх 2 ду 2
z ~% <?f ' d(x,y) V ( ) Vi/f = V 2 (Vfy)
and no
4
Two-dimensiona (planar) Cylindrical Vy — (V ф) Н — v4 ф (В) - \ \дх 4 +2 дх ду 2 + ду /
дф
A
z-dependence
d
)ф
д
д
2
4
= 0
with v
r dQ
z
with no
z-dependence ~ дф
Cylindrical r 2 z Е - \ \ t + \
д
д
2
with
0
t7 -
metrical and no 0 ^^ 6?(r,z) r ^ dY Г ° r dz
0-dependence
xisym Spherical О r 2 sin 0 дф д 2 2 1 ^V*A/ ^ ДО £ 2 _ д 2 Sin0 д ( 1 д\
1
/
г 2 / \
-i/
with у
=
dQ
ф
< and no <?f r s i n 0 <?(r, 0) dr 2 ( Y 2 дв \ Sin 0 дв)
ф-dependence V °~ + r s i n 0 dr I ^^ ^ " ->л si n t/ I — vtL
Y sin 0 \ *" ^^ / W \LJ)
" Similar relations in general orthogonal coordinates may be found in S. Goldstein, Modern Developments in Fluid Dynamics, Dover, N.Y. (1965), pp. 114-115; in
this reference, formulas are also given for axisymmetrical flows with a nonzero component of the velocity around the axis.
b
Here the Jacobians are designated by
CD
df/дх df/dy
д(х, у) dg/dy

о