Page 166 - Bird R.B. Transport phenomena

150 Chapter 4 Velocity Distributions with More Than One Independent Variable

(a) Find the pressure distribution, radial flow velocity, and mass rate of flow for an incom-
pressible fluid.
(b) Rework (a) for a compressible liquid and for an ideal gas.
<3> 2тгкНр ~
Answers: (a) - 2 w = 2
In (R /R,) /x In (R /R )
2
x
2
4D.1 Flow near an oscillating wall. 8 Show, by using Laplace transforms, that the complete solu-
tion to the problem stated in Eqs. 4.1-44 to 47 is
- ^ <r '(sirr — dw (4D.1-1)
w
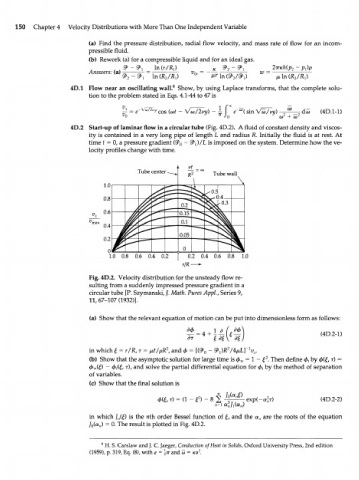
4D.2 Start-up of laminar flow in a circular tube (Fig. 4D.2). A fluid of constant density and viscos-
ity is contained in a very long pipe of length L and radius R. Initially the fluid is at rest. At
time t = 0, a pressure gradient (0> - 2P )/L is imposed on the system. Determine how the ve-
o
L
locity profiles change with time.
Tube center Tube wall
\

1.0 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1.0

Fig. 4D.2. Velocity distribution for the unsteady flow re-
sulting from a suddenly impressed pressure gradient in a
circular tube [P. Szymanski, /. Math. Pures Appl., Series 9,
11,67-107(1932)].

(a) Show that the relevant equation of motion can be put into dimensionless form as follows:

(4D.2-1)

2
in which £ = r/R, т = fit/pR , and ф = [&
0
f
(b) Show that the asymptotic solution for large time is ф х = 1 - . 2 Then define ф, by ф(£, т) =
фоо(& ~ Ф((С т), and solve the partial differential equation for ф by the method of separation
{
of variables.
(c) Show that the final solution is
2
ф((, г) = (1 - f ) - 8 ехр(-а т) (4D.2-2)
2
in which /„(£) is the nth order Bessel function of £, and the a n are the roots of the equation
Jota,,) = 0. The result is plotted in Fig. 4D.2.

8
H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, Oxford University Press, 2nd edition
(1959), p. 319, Eq. (8), with e = ^