Page 182 - Bird R.B. Transport phenomena

166 Chapter 5 Velocity Distributions in Turbulent Flow

more important over most of the cross section and that the viscous contribution is im-
portant only in the vicinity of the wall. This is further illustrated in Example 5.5-3. Anal-
ogous behavior is observed in tubes of circular cross section.

EXAMPLE 5.5-1 Apply the results of §5.3 to obtain the average velocity for turbulent flow in a circular tube.

Estimation of the SOLUTION
Average Velocity
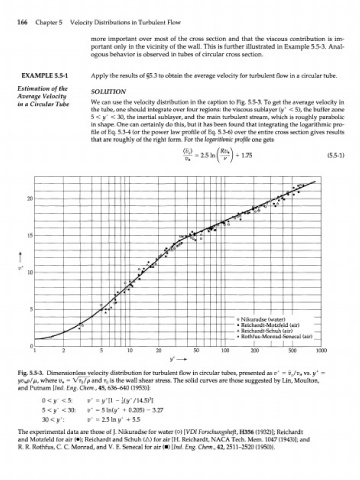
in a Circular Tube We can use the velocity distribution in the caption to Fig. 5.5-3. To get the average velocity in
the tube, one should integrate over four regions: the viscous sublayer (y + < 5), the buffer zone
5 < y + < 30, the inertial sublayer, and the main turbulent stream, which is roughly parabolic
in shape. One can certainly do this, but it has been found that integrating the logarithmic pro-
file of Eq. 5.3-4 (or the power law profile of Eq. 5.3-6) over the entire cross section gives results
that are roughly of the right form. For the logarithmic profile one gets

1.75 (5.5-1)

1 ***

• •
20
Ф Л
^ \
4 о
15
о
г
i tj.
10 &*-
с X
jr A
в.
/
5 A
A
о Niku radse (water)
• Reich ardt-Motzfeld (ciir) —
л Reich ardt-Schuh (air)
* Rothius-Monrad-Senecal (air)
n
10 20 50 100 200 500 1000

Fig. 5.5-3. Dimensionless velocity distribution for turbulent flow in circular tubes, presented as v + = vjv* vs. y + =
yv+p/fju, where v* = Vr /p and т is the wall shear stress. The solid curves are those suggested by Lin, Moulton,
o
0
and Putnam [Ind. Eng. Chem., 45, 636-640 (1953)]:
+
+
3
0 < y' < 5: v + = у П ~ \{y /14.5) ]
5 < y^ < 30: v + = 5 ln(y + + 0.205) - 3.27
+
30<y : zT =2.51ny+ +55
The experimental data are those of J. Nikuradse for water (o) [VDI Forschungsheft, H356 (1932)]; Reichardt
and Motzfeld for air (•); Reichardt and Schuh (Л) for air [H. Reichardt, NACA Tech. Mem. 1047 (1943)]; and
R. R. Rothfus, С. С Monrad, and V. E. Senecal for air (•) [Ind. Eng. Chem., 42,2511-2520 (1950)}.