Page 272 - Bird R.B. Transport phenomena

256 Chapter 8 Polymeric Liquids

10,000

• К 1000 -

II

10 100 1000 10 100 1000
1
1
Shear rate у (s" ) Shear rate у (s" )
(a) (b)
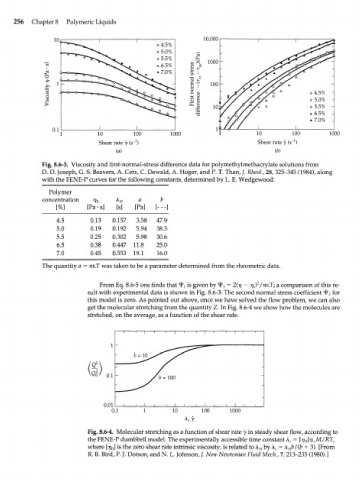
Fig. 8.6-3. Viscosity and first-normal-stress difference data for polymethylmethacrylate solutions from
D. D. Joseph, G. S. Beavers, A. Cers, C. Dewald, A. Hoger, and P. T. Than, /. RheoL, 28,325-345 (1984), along
with the FENE-P curves for the following constants, determined by L. E. Wedgewood:

Polymer
concentration Vo AH a b
[%] [Pa • s] [s] [Pa] [---]
4.5 0.13 0.157 3.58 47.9
5.0 0.19 0.192 5.94 38.3
55 0.25 0.302 5.98 30.6
6.5 0.38 0.447 11.8 25.0
7.0 0.45 0.553 19.1 16.0
The quantity a = пкТ was taken to be a parameter determined from the rheometric data.

From Eq. 8.6-5 one finds that "^ is given by ^ = 2(17 - т] ) /пкТ; a comparison of this re-
2
$
sult with experimental data is shown in Fig. 8.6-3. The second normal stress coefficient ^ 2 f° r
this model is zero. As pointed out above, once we have solved the flow problem, we can also
get the molecular stretching from the quantity Z. In Fig. 8.6-4 we show how the molecules are
stretched, on the average, as a function of the shear rate.

0.01
1000
К У
Fig. 8.6-4. Molecular stretching as a function of shear rate у in steady shear flow, according to
the FENE-P dumbbell model. The experimentally accessible time constant \ c = [r] ]r] M/RT,
0
s
where [TJQ] is the zero shear rate intrinsic viscosity, is related to A by \ c = X b/(b + 3). [From
H
H
R. B. Bird, P. J. Dotson, and N. L. Johnson, /. Non-Newtonian Fluid Mech., 7,213-235 (1980).]