Page 273 - Bird R.B. Transport phenomena

.6 Molecular Theories for Polymeric Liquids 257

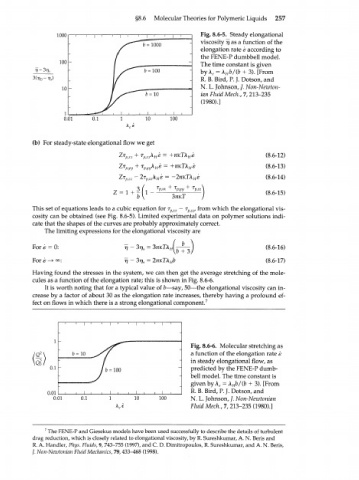
Fig. 8.6-5. Steady elongational
JUU i i | i i | 1 1 1 1 1 1 1
viscosity rjasa function of the
/ ^ ~ ~b = 1000 elongation rate s according to
/
the FENE-P dumbbell model.
100 - The time constant is given
V - Зт], / ^ b = 100 byA e = A b/(b + 3). [From
H
R. B. Bird, P. J. Dotson, and
10 N. L. Johnson, /. Non-Newton-
ian Fluid Mech., 7,213-235
(1980).]
1 ._! L_=—4-" l 1 I 1 , 1 1 I
0.01 0.1 1 10 100

(b) For steady-state elongational flow we get
+ r P/XX X H s = (8.6-12)
Z T P I X X
ZTp,yy + p,yi/H€ = +ПКТ\ £ (8.6-13)
T
Н
- 2T PIZZ\ HS = -2пкТ\ н е (8.6-14)
ZT PIZZ
3 Л _ V Т Р,УУ + P,Z2 (8.6-15)
T
ЗпкТ
This set of equations leads to a cubic equation for r pxx - r P/ZZ/ from which the elongational vis-
cosity can be obtained (see Fig. 8.6-5). Limited experimental data on polymer solutions indi-
cate that the shapes of the curves are probably approximately correct.
The limiting expressions for the elongational viscosity are

For s = 0: г] - = ЗпкГЛ | н (8.6-16)
For ir = 2пкТХ Ь (8.6-17)
н
Having found the stresses in the system, we can then get the average stretching of the mole-
cules as a function of the elongation rate; this is shown in Fig. 8.6-6.
It is worth noting that for a typical value of b—say, 50—the elongational viscosity can in-
crease by a factor of about 30 as the elongation rate increases, thereby having a profound ef-
fect on flows in which there is a strong elongational component. 7

1 ' 1 1 i i | i i | i

-1 Fig. 8.6-6. Molecular stretching as
1- in steady elongational flow, as
b =10 a function of the elongation rate e

0.1 - 100 predicted by the FENE-P dumb-
bell model. The time constant is
H
- given by A, = \ b/(b + 3). [From
0 01 1 1 \ i 1 i l l i l l R. B. Bird, P. J. Dotson, and
0.01 0.1 10 100 N. L. Johnson, /. Non-Newtonian
Fluid Mech., 7,213-235 (1980).]

The FENE-P and Giesekus models have been used successfully to describe the details of turbulent
7
drag reduction, which is closely related to elongational viscosity, by R. Sureshkumar, A. N. Beris and
R. A. Handler, Phys. Fluids, 9, 743-755 (1997), and C. D. Dimitropoulos, R. Sureshkumar, and A. N. Beris,
/. Non-Newtonian Fluid Mechanics, 79, 433^68 (1998).