Page 458 - Bird R.B. Transport phenomena

438 Chapter 14 Interphase Transport in Nonisothermal Systems

Note that in this problem we did not have to calculate h. Numerical evaluation of h is
necessary, however, in more complicated problems such as heat exchange between two fluids
with an intervening wall.

§144 HEAT TRANSFER COEFFICIENTS FOR FORCED
CONVECTION AROUND SUBMERGED OBJECTS
Another topic of industrial importance is the transfer of heat to or from an object around
which a fluid is flowing. The object may be relatively simple, such as a single cylinder or
sphere, or it may be more complex, such as a "tube bundle" made up of a set of cylindri-
cal tubes with a stream of gas or liquid flowing between them. We examine here only a
few selected correlations for simple systems: the flat plate, the sphere, and the cylinder.
Many additional correlations may be found in the references cited in the introduction to
the chapter.

Flow Along a Flat Plate

We first examine the flow along a flat plate, oriented parallel to the flow, with its surface
maintained at T o and the approaching stream having a uniform temperature T K and a
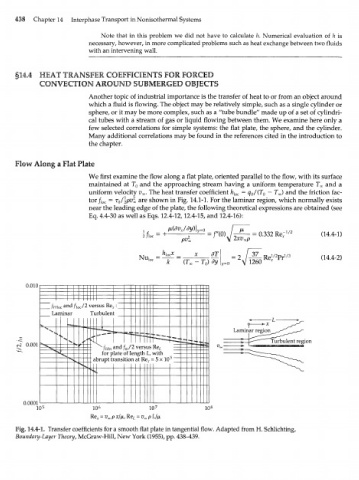
uniform velocity v . The heat transfer coefficient /z loc = q /(T o — T^) and the friction fac-
x
o
V1
tor /ioc = T Q/\P K a r e shown in Fig. 14.1-1. For the laminar region, which normally exists
near the leading edge of the plate, the following theoretical expressions are obtained (see
Eq. 4.4-30 as well as Eqs. 12.4-12,12.4-15, and 12.4-16):
-1/2
= 0.332 Re; (14.4-1)

Nu = (14.4-2)
к (Г. - Т )
lo c
о
0.010

/H loc a n d /loc/ 2 versusRe A
Lciminar Turbulen t

\
ESQ.
_ a: v oa Turbulent region
c? 0.001 it f 1 0 jrCll с l?o.
JHm " AlVA ;m / *• * > - ^ " ^ A ^ L
А
for plate of length L, with
abn apt transition at Re Y = 5x10

0,0001
105 10 6 10 7 10 8
= =
Re x v 0 , Re L v o
Fig. 14.4-1. Transfer coefficients for a smooth flat plate in tangential flow. Adapted from H. Schlichting,
Boundary-Layer Theory, McGraw-Hill, New York (1955), pp. 438-439.