Page 623 - Bird R.B. Transport phenomena

§19.5 Dimensional Analysis of the Equations of Change for Nonreacting Binary Mixtures 603

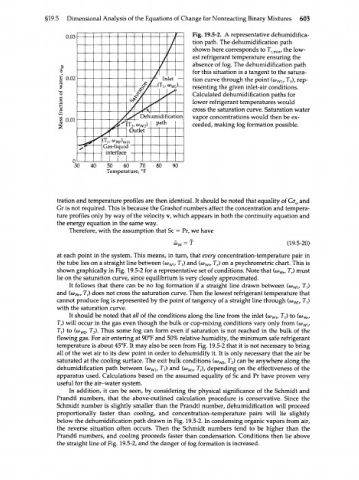
0.03 у г Fig. 19.5-2. A representative dehumidifica-
/ tion path. The dehumidification path low-
here corresponds
T, , the
to
shown
min
/ est refrigerant temperature ensuring the
f absence of fog. The dehumidification path
for this situation is a tangent to the satura-
0.02 / т „ tion curve through the point (w , Tj), rep-
f Iniei ,) wi
( resenting the given inlet-air conditions.
Calculated dehumidification paths for
t/ lower refrigerant temperatures would water
cross the saturation curve. Saturation
« o.oi л )ehumidif cation vapor concentrations would then be ex-
ath
A (T 2/ w M P ceeded, making fog formation possible.
'Л Outlet
in
Gas-liqui( d
jpf<srfar"<3
0
30 40 50 60 70 80 90
Temperature, °F

tration and temperature profiles are then identical. It should be noted that equality of Gr and
w
Gr is not required. This is because the Grashof numbers affect the concentration and tempera-
ture profiles only by way of the velocity v, which appears in both the continuity equation and
the energy equation in the same way.
Therefore, with the assumption that Sc = Pr, we have
= T (19.5-20)
at each point in the system. This means, in turn, that every concentration-temperature pair in
the tube lies on a straight line between (<o , TJ and (w , T ) on a psychrometric chart. This is
Wr
r
m
shown graphically in Fig. 19.5-2 for a representative set of conditions. Note that (ш , T ) must
т
r
lie on the saturation curve, since equilibrium is very closely approximated.
It follows that there can be no fog formation if a straight line drawn between (o) , T )
}
m
and (a) , T,) does not cross the saturation curve. Then the lowest refrigerant temperature that
Wr
cannot produce fog is represented by the point of tangency of a straight line through (to , T )
}
m
with the saturation curve.
It should be noted that all of the conditions along the line from the inlet (a) , T ) to (a) ,
A
Wr
m
T ) will occur in the gas even though the bulk or cup-mixing conditions vary only from (<o ,
r
m
T ) to (WWJ, T ). Thus some fog can form even if saturation is not reached in the bulk of the
x
2
flowing gas. For air entering at 90°F and 50% relative humidity, the minimum safe refrigerant
temperature is about 45°F. It may also be seen from Fig. 19.5-2 that it is not necessary to bring
all of the wet air to its dew point in order to dehumidify it. It is only necessary that the air be
saturated at the cooling surface. The exit bulk conditions (о>^, ^г) can be anywhere along the
dehumidification path between (w , TJ and (<o , T ), depending on the effectiveness of the
r
wl
Wr
apparatus used. Calculations based on the assumed equality of Sc and Pr have proven very
useful for the air-water system.
In addition, it can be seen, by considering the physical significance of the Schmidt and
Prandtl numbers, that the above-outlined calculation procedure is conservative. Since the
Schmidt number is slightly smaller than the Prandtl number, dehumidification will proceed
proportionally faster than cooling, and concentration-temperature pairs will lie slightly
below the dehumidification path drawn in Fig. 19.5-2. In condensing organic vapors from air,
the reverse situation often occurs. Then the Schmidt numbers tend to be higher than the
Prandtl numbers, and cooling proceeds faster than condensation. Conditions then lie above
the straight line of Fig. 19.5-2, and the danger of fog formation is increased.