Page 355 - Tunable Lasers Handbook

7 Optical Parametric OsciIIators 3 1 5

Birefringence angles can be calculated in uniaxial crystals given the ordi-
nary and evtraordinary indices of refraction, ri0 and ne. respectively [20]. In a
given direction of propagation. there are two refractive indices for the two
polarizations. Specifying a direction of propagation 8 and the two refractive
indices, denoted by and 17,. a refractive index for the extraordinary polarized
ray can be calculated, similar to the calculations used for phase matching. With
these, the birefringence angle in an uniaxial crystal can be expressed as

In an uniaxial crystal. the angle p is measured in the optic plane. In a biaxial
crystal, a similar analysis can yield the birefringence angle.
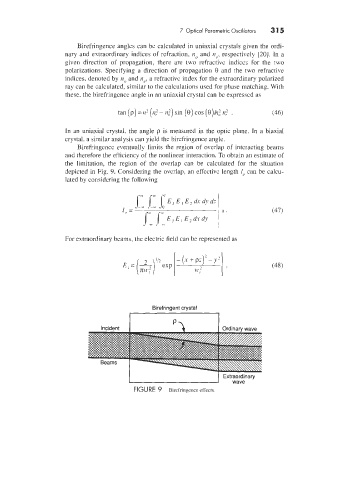
Birefringence eventually limits the region of overlap of interacting beams
and therefore the efficiency of the nonlinear interaction. To obtain an estimate of
the limitation, the region of the overlap can be calculated for the situation
depicted in Fig. 9. Considering the overlap. an effective length le can be calcu-
lated by considering the folloning

(47 j

For extraordinary beams, the electric field can be represented as

Birefringent crystal
I 1

I ExtrFarddary

FIGURE 9 Birefringence effects.