Page 486 - Tunable Lasers Handbook

446 Stephen Vincent Benson

1

U
-
w
.- o
m
E
z" -0.5
-1
-16.0 0.00 16.0
Wavelength detuning
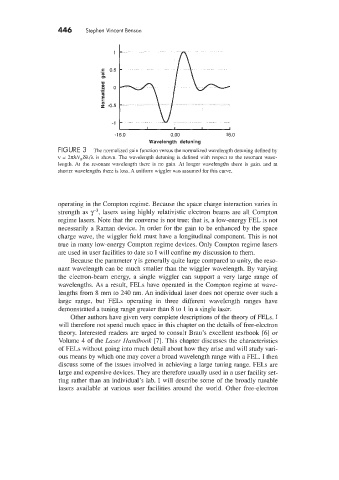
FIGURE 3 The normalized gain function versus the normalized wavelength detuning defined by
v = 2~chV,$,,/k is shown. The wavelength detuning is defined with respect to the resonant wave-
length. At the resonant wavelength there is no gain. At longer wavelengths there is gain. and at
shorter Lvavelengths there is loss. 4 uniform wiggler was assumed for this curve.

operating in the Compton regime. Because the space charge interaction varies in
strength as y', lasers using highly relativistic electron beams are all Compton
regime lasers. Note that the converse is not true: that is, a low-energy FEL is not
necessarily a Raman device. In order for the gain to be enhanced by the space
charge wave, the wiggler field must have a longitudinal component. This is not
true in many low-energy Compton regime devices. Only Compton regime lasers
are used in user facilities to date so I will confine my discussion to them.
Because the parameter y is generally quite large compared to unity, the reso-
nant wavelength can be much smaller than the wiggler wavelength. By varying
the electron-beam energy, a single wiggler can support a very large range of
wavelengths. As a result, FELs have operated in the Compton regime at wave-
lengths from 8 mm to 240 nm. An individual laser does not operate over such a
large range, but FELs operating in three different wavelength ranges have
demonstrated a tuning range greater than 8 to 1 in a single laser.
Other authors have given very complete descriptions of the theory of FELs. I
will therefore not spend much space in this chapter on the details of free-electron
theory. Interested readers are urged to consult Brau's excellent textbook [6] or
Volume 4 of the Laser Handbook [7]. This chapter discusses the characteristics
of FELs without going into much detail about how they arise and will shdy vari-
ous means by which one may cover a broad wavelength range with a FEL. I then
discuss some of the issues involved in achieving a large tuning range. FELs are
large and expensive devices. They are therefore usually used in a user facility set-
ting rather than an individual's lab. I will describe some of the broadly tunable
lasers available at various user facilities around the world. Other free-electron