Page 99 - Using ANSYS for Finite Element Analysis Dynamic, Probabilistic, Design and Heat Transfer Analysis

86 • using ansys for finite eLement anaLysis
where s is the shape parameter, q is the location parameter, and m is the
scale parameter. The case where q = 0 and m = 1 is called the standard log-
normal distribution. The equation for the standard normal distribution is:

2s
e −( ln x ()) 2 / ( )
2
fx () = � x ≥ 0,s > 0
xs 2p
Since the general form of probability functions can be expressed in
terms of the standard distribution, all subsequent formulas in this section
are given for the standard form of the function.
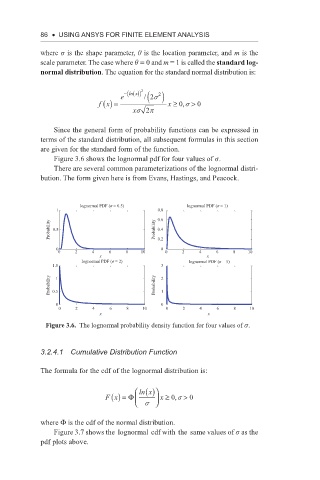
Figure 3.6 shows the lognormal pdf for four values of s.
There are several common parameterizations of the lognormal distri-
bution. The form given here is from Evans, Hastings, and Peacock.

lognormal PDF (σ = 0.5) lognormal PDF (σ = 1)
1 0.8
0.6
Probability 0.5 Probability 0.4
0.2
0 0
0 2 4 6 8 10 0 2 4 6 8 10
x x
lognormal PDF (σ = 2) lognormal PDF (σ = 5)
1.5 3
Probability 0.5 1 Probability 2 1

0 0
0 2 4 6 8 10 0 2 4 6 8 10
x x
Figure 3.6. The lognormal probability density function for four values of s.

3.2.4.1 Cumulative Distribution Function

The formula for the cdf of the lognormal distribution is:

 ln x ()
Fx () = Φ   s   � x ≥ 0, s > 0

where F is the cdf of the normal distribution.
Figure 3.7 shows the lognormal cdf with the same values of s as the
pdf plots above.