Page 100 - Using ANSYS for Finite Element Analysis Dynamic, Probabilistic, Design and Heat Transfer Analysis
P. 100
probabilistic Design analysis • 87
lognormal PDF (σ = 0.5) lognormal PDF (σ = 1)
1 1
Probability 0.5 Probability 0.5
0 0
0 2 4 6 8 10 0 2 4 6 8 10
x x
lognormal PDF (σ = 2) lognormal PDF (σ = 5)
1 0.8
0.6
Probability 0.5 Probability 0.4
0.2
0 0
0 2 4 6 8 10 0 2 4 6 8 10
x x
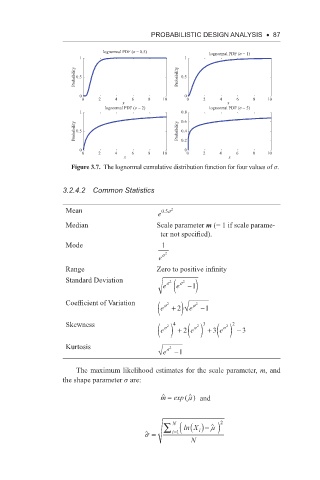
Figure 3.7. The lognormal cumulative distribution function for four values of s.
3.2.4.2 Common Statistics
Mean e 05s 2
.
Median Scale parameter m (= 1 if scale parame-
ter not specified).
Mode 1
e s 2
Range Zero to positive infinity
Standard Deviation 2 2
e s ( e s − 1 )
( e s 2 + 2 ) e s 2 − 1
Coefficient of Variation
Skewness ( ) ( ) ( ) − 3
2 2
2 4
2 3
s
s
s
+
e
e
e
+
3
2
Kurtosis 2
e s − 1
The maximum likelihood estimates for the scale parameter, m, and
the shape parameter s are:
∧
∧
m = exp() and
m
∑ N ( ln ( ) −X m ) 2
∧
∧ s = = i 1 i
N