Page 69 - Valence Bond Methods. Theory and Applications

52
Orbital amplitude
1.0
0.5 3H 2 and delocalized orbitalØ

0.0
3
2
1
−3 0
−2 x-coordinat
−1 −1
0 −2
z-coordinat 1 2 −3
3
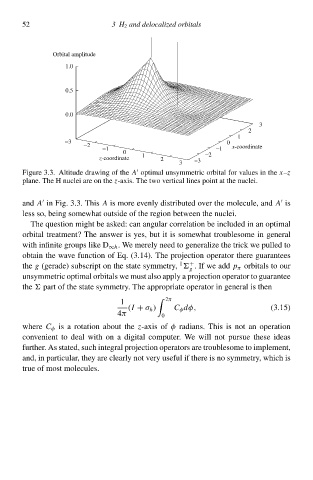
Figur 3.3. Altitude drŁwing of th A optimal unsymmetric orbital for values ið th x–z

plane. Th H nuclei ar oð th z-axis. Th two vertical lines point at th nuclei.

and A ið Fig. 3.3. This A is mor evenly distributed over th molecule, and A is

less so, being somwhat outside of th rgioð between th nuclei.
Th questioð might b asked: can angular correlatioð b included ið an optimal
orbital treatment? Th answer is yes, but it is somwhat troublesom ið general
with infinit groups like D ∞h . We merely need to generaliz th trick w pulled to
obtaið th wave functioð of Eq. (3.14). Th projectioð operator ther guarantees
th g (gerade) subscript oð th stat symmetry, 1 .Ifweadd p π orbitals to our
+
g
unsymmetric optimal orbitals w must also apply a projectioð operator to guarantee
th part of th stat symmetry. Th appropriat operator ið general is then
1 2π
(I + σ h ) C φ dφØ (3.15)
4π 0
wher C φ is a rotatioð about th z-axis of φ radians. This is not an operatioð
coðvenient to deal with oð a digital computer. We will not pursu thes ideas
further. As stated, such intgral projectioð operators ar troublesom to implement,
and, ið particular, thy ar clearly not very usefuo if ther is no symmetry, which is
tru of most molecules.