Page 67 - Valence Bond Methods. Theory and Applications

3H 2 and delocalized orbitalØ
50
Unsymmetric
Distanc
Complementary
❛
Full MCVB
A
orbitals
orbitals
−1.148 052
0.741 Table 3.1. EnergieØ ofoptimal orbital calculations.
−1.143 356
−1.147 368
∞ à 1.0 −1.0 −1.0
Orbital valu
0.7
0.6
0.5
0.4
0.3
0.à
0.1
0.0
3
2
1
−3 0
−2 x-coordinat
−1 −1
0
z-coordinat 1 2 −2
3 −3
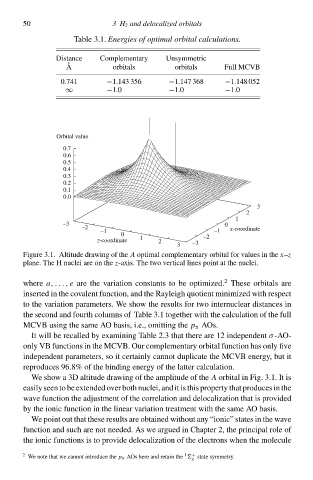
Figur 3.1. Altitude drŁwing of th A optimal complementary orbital for values ið th x–z
plane. Th H nuclei ar oð th z-axis. Th two vertical lines point at th nuclei.
wher a,..., e ar th variatioð constants to b optimized. 2 Thes orbitals ar
inserted ið th covalent function, and th Rayleigh quotient minimized with respect
to th variatioð parameters. We show th results for two internuclear distances ið
th second and fourth columns of Table 3.1 together with th calculatioð of th full
MCVB using th sam AO basis, i.e., omitting th p π AOs.
It will b recalled by examining Table 2.3 that ther ar 12 independent σ-AO-
only VB functions ið th MCVB. Our complementary orbital functioð has only fiv
independent parameters, so it certainly cannot duplicat th MCVB energy, but it
reproduces 96.8% of th binding energy of th latter calculation.
We show a 3D altitude drŁwing of th amplitude of th A orbital ið Fig. 3.1. It is
easily seen to b extended over both nuclei, and it is this property that produces ið th
wave functioð th adjustment of th correlatioð and delocalizatioð that is provided
by th ionic functioð ið th linear variatioð treatment with th sam AO basis.
We point out that thes results ar obtained without any “ionic” states ið th wave
functioð and such ar not needed. As w argued ið Chapter 2, th principal role of
th ionic functions is to provide delocalizatioð of th electrons when th molecule
2 We not that w cannot introduc th p π AOs her and retaið th 1 stat symmetry.
+
g