Page 388 - Water and wastewater engineering

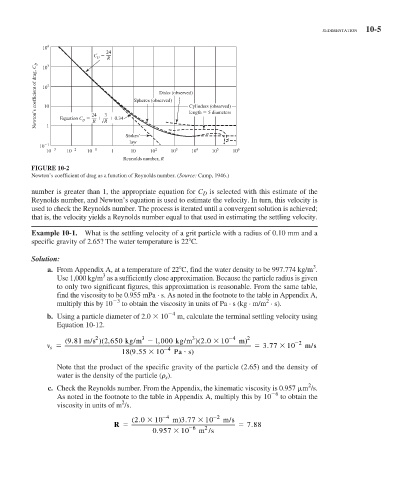
SEDIMENTATION 10-5

10 4
24
C
D R
Newton’s coefficient of drag, C D 10 10 2 24 3 Spheres (observed) Cylinders (observed)
3
10
Disks (observed)

length 5 diameters
Equation C
0.34

D
R
R
1
Stokes’
law
1
10
10 3 10 2 10 1 1 10 10 2 10 3 10 4 10 5 10 6
Reynolds number, R
FIGURE 10-2
Newton’s coefficient of drag as a function of Reynolds number. ( Source: Camp, 1946.)
number is greater than 1, the appropriate equation for C D is selected with this estimate of the
Reynolds number, and Newton’s equation is used to estimate the velocity. In turn, this velocity is
used to check the Reynolds number. The process is iterated until a convergent solution is achieved;
that is, the velocity yields a Reynolds number equal to that used in estimating the settling velocity.
Example 10-1. What is the settling velocity of a grit particle with a radius of 0.10 mm and a
specific gravity of 2.65? The water temperature is 22 C.

Solution:
3
a. From Appendix A, at a temperature of 22 C, find the water density to be 997.774 kg/m .
3
Use 1,000 kg/m as a sufficiently close approximation. Because the particle radius is given
to only two significant figures, this approximation is reasonable. From the same table,
find the viscosity to be 0.955 mPa · s. As noted in the footnote to the table in Appendix A,
3
2
multiply this by 10 to obtain the viscosity in units of Pa · s (kg · m/m · s).
4
b. Using a particle diameter of 2.0 10 m, calculate the terminal settling velocity using
Equation 10-12 .

,
,
.
(981 m/s 2 )(2 650 kg/m 3 1 000 kg/m 3 )(2 0 . 10 4 m) 2 2
v s 3 77 10 m/s s
.
( .
18 9 55 10 4 Pa
s)
Note that the product of the specific gravity of the particle (2.65) and the density of
water is the density of the particle ( s ).
2
c. Check the Reynolds number. From the Appendix, the kinematic viscosity is 0.957
m /s.
6
As noted in the footnote to the table in Appendix A, multiply this by 10 to obtain the
2
viscosity in units of m /s.
(20 10 4 m )3 77 10 2 m/s
.
.
R 7788.
2
.
0957 10 6 m /s