Page 260 - Whole Earth Geophysics An Introductory Textbook For Geologists And Geophysicists

~
Examples of lithospheric
bulges
accretionary
plates
“flexural”
where
amplitude
equation
both
plate
plate
crust.
a
243
a
plate
of
At
edge
8.24.
in
of the
lithospheric
downgoing
oceanic
4)
3)
flexural
lsostasy
expressed
depression;
above
wavelength;
the
or
Fig.
small
surface
the
( “peripheral”
the
at
in
thickness.
and
the
bending
a
of
shown
the
on
weak
8.24
be
have
the
topography
to
mountains
bulge
a
of
can
smaller
FIGURE
by
on
solutions
a
will
Flexure
are
the
considerable
that
point
separated
2)
equilibrium.
a
deflection
x.
flexure
sea,
wavelength;
plate
D)
plate
to
a
plate
at
a
over
the
the
analogous
to
plate.
(large
plate
to
by
the
the
out
load
primarily
Joad,
a
lithospheric
illustrated
between
but
on
below
the
above
to
upward
farther
isostatic
overriding
plate
the
sediment
w),
long
load
of
acceleration
the
is
from
top
material
material
lithospheric
(large
flexure
is
Depressions
from
and,
a
a
an
are
local
load
puts
the
over
of
distance
strength,
the
a
with
(trench)
concepts
examples
distance
deflection
to
8.24a),
into
The
mountains
the
the
spread
on
gravitational
applied
fill
horizontal
of
of
collapse
8.22).
strong
arc
can
8.24b).
significant
density
density
depression
some
(Fig.
important
w),
simplified
volcanic
large
load
basins”)
(Fig.
high
a
(small
zone
strength
develops
(Fig.
1)
=
=
=
=
=
has
board
of
Pp,
g
Pp,
x
8.23b):
q(x)
have
and
subduction
(‘foreland
a
Four
directions
deflection
Two
D)
mass
in
no
results
bulge)
diving
wedge
(small
plates
(Fig.
with
The
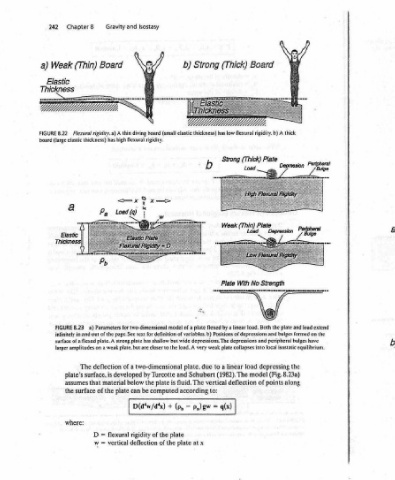
a) Zone Subduction bulge and flexural flexure. a) A <9 ¥ ” ot the (trench) develop as depression 4 ws & > at a subduction flexed is downgoing plate zone.b) The = : Ye <a range mountain of a weight with fill depressions that causes adjacent basins). (foreland sediment ~N Foreland Load "Boe Basin (Mountains)

load extend the
i bulges have isostatic equilibrium.
thick Depression the plate and bulges formed on peripheral the (Fig. 8.23a) along
rigidity. b) A Plate (Thick) Load Strength No With linear load. Both Positions of depressions and depressing load model The of points deflection
elastic thickness) has low flexural Strong b Plate flexed by a plate of variables. b) depressions. The depressions and very weak plate collapses into local linear a to due (1982). Schubert vertical The to: according q(x) = p,) gw x at
(small model of a for definition wide but Joad. A are closer to the plate. and by Turcotte is fluid. plate plate computed — (p, + plate of the plate the of
lsostasy diving board rigidity. text has shallow two-dimensional the be D(d‘w/d‘x) rigidity deflection
and thin flexural Parameters for two-dimensional strong plate plate. but a of developed below can
Gravity has high of the page. See plate. A weak a deflection material the flexural vertical
Ml
8 Flexural rigidity. a) A a) flexed The surface, is that of surface A 2
Chapter (large elastic thickness) 8.23 infinitely in and out surface of a larger amplitudes on plate’s assumes the where:
242 Elastic Thickness 8.22 FIGURE board FIGURE