Page 262 - Whole Earth Geophysics An Introductory Textbook For Geologists And Geophysicists

Earth from
the
Analogy between
245
gravitational auraction of the
Modeling
8.26
Gravity
FIGURE
b
|
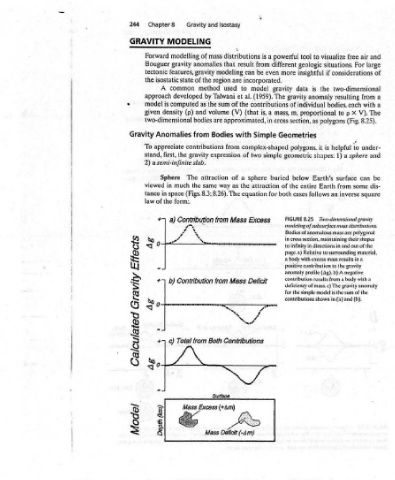
and Surface Earth's space and a sphere of anomalous mass Earth's a) Earth's surface. buried beneath large (g) at a distant acceleration gravitational of mass of the depends on point observation from (R) the distance (M) and Earth the to the observation the center of mass (Ag) due gravity in point. b) The change a the to a buried sphere depends on a to the mass (Am, relative in differ
air For from with V). 8.25). can some polygonal
free considerations two-dimensional resulting bodies, each X p (Fig. to sphere a surface from inverse Tivo-dimensional gravity and out of the to surrounding material, to the gravity negative the sum of the (a) and (b).
visualize situations. if to polygons helpful is 1) Earth an modeling of subsurface mass distributions. in cross section, maintaining their shapes body with excess mass results in a results from a body with a deficiency of mass. c) The gravity anomaly model is in
to insightful is the anomaly individual proportional as it shapes: Earth’s follows Bodies of anomalous mass are to infinity in directions in Relative anomaly profile (Ag). b) A
tool geologic data gravity section, Geometries polygons, geometric below entire cases 8.25 positive contribution contribution the simple contributions shown
powerful different more gravity of m, mass, cross buried the of both FIGURE page. a) a for
a even (1959). The contributions a in simple for
is from be incorporated. model is, Simple complex-shaped two sphere attraction equation Excess Deficit / Z
distributions result can are to al. et the (V) (that approximated, with of a the Mass Mass NA Contributions A> Deficit (-Am)

Isostasy that modeling region used of sum Bodies from expression of way as The from trom as SK

and Gravity mass of anomalies gravity of the method by Talwani the as volume and are bodies from contributions gravity attraction The same the (Figs. 8.3; 8.26). Contribution x % Ne Contribution Both Total from Surface Excess (+Am) Mass
Chapter8 244 MODELING GRAVITY modelling Forward gravity Bouguer features, tectonic isostatic state the A common developed approach computed is model (p) density given two-dimensional Gravity Anomalies appreciate To the first, stand, a semi-infinite slab. 2) Sphere much in viewed space in tance form: the of law a) +7 eos sjoeyy AUAeID peyeynajeg [Epon

Mass

ww
b)
¢)
(un) yideq
+>
+>
S
dy
X
aU

| |