Page 358 - Wind Energy Handbook

332 CONCEPTUAL DESIGN OF HORIZONTAL-AXIS TURBINES

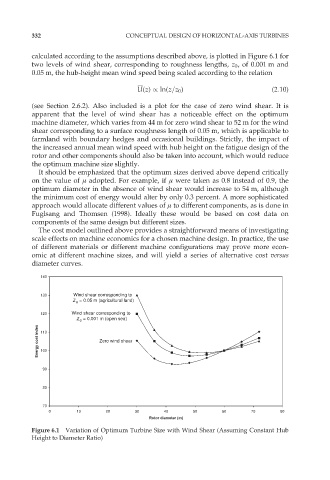
calculated according to the assumptions described above, is plotted in Figure 6.1 for
two levels of wind shear, corresponding to roughness lengths, z 0 , of 0.001 m and
0.05 m, the hub-height mean wind speed being scaled according to the relation

U(z) / ln(z=z 0 ) (2:10)

(see Section 2.6.2). Also included is a plot for the case of zero wind shear. It is
apparent that the level of wind shear has a noticeable effect on the optimum
machine diameter, which varies from 44 m for zero wind shear to 52 m for the wind
shear corresponding to a surface roughness length of 0.05 m, which is applicable to
farmland with boundary hedges and occasional buildings. Strictly, the impact of
the increased annual mean wind speed with hub height on the fatigue design of the
rotor and other components should also be taken into account, which would reduce
the optimum machine size slightly.
It should be emphasized that the optimum sizes derived above depend critically
on the value of ì adopted. For example, if ì were taken as 0.8 instead of 0.9, the
optimum diameter in the absence of wind shear would increase to 54 m, although
the minimum cost of energy would alter by only 0.3 percent. A more sophisticated
approach would allocate different values of ì to different components, as is done in
Fuglsang and Thomsen (1998). Ideally these would be based on cost data on
components of the same design but different sizes.
The cost model outlined above provides a straightforward means of investigating
scale effects on machine economics for a chosen machine design. In practice, the use
of different materials or different machine configurations may prove more econ-
omic at different machine sizes, and will yield a series of alternative cost versus
diameter curves.

140

130 Wind shear corresponding to
Z o = 0.05 m (agricultural land)
120 Wind shear corresponding to
= 0.001 m (open sea)
Z o
Energy cost index 110 Zero wind shear

100

90

80

70
0 10 20 30 40 50 60 70 80
Rotor diameter (m)
Figure 6.1 Variation of Optimum Turbine Size with Wind Shear (Assuming Constant Hub
Height to Diameter Ratio)