Page 34 - Characterization and Properties of Petroleum Fractions - M.R. Riazi
P. 34
T1: IML
QC: IML/FFX
P2: IML/FFX
P1: IML/FFX
AT029-01
June 22, 2007
AT029-Manual
AT029-Manual-v7.cls
14:26
14 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
where N min is the minimum number of plates, and x D and x B
are the mole fraction of the light component in the distillate
n (top) and bottom products, respectively. Equation (1.5) is de-
n veloped for a binary mixture; however, a similar equation has
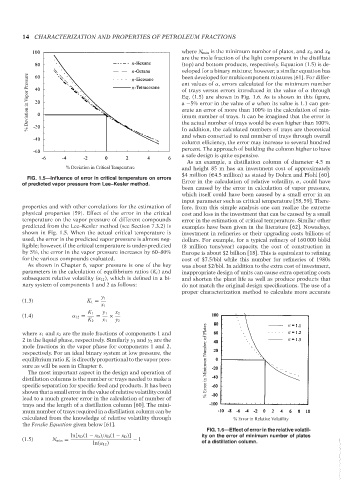
% Deviation in Vapor Pressure n of trays versus errors introduced in the value of α through
been developed for multicomponent mixtures [61]. For differ-
n
ent values of α, errors calculated for the minimum number
Eq. (1.5) are shown in Fig. 1.6. As is shown in this figure,
a −5% error in the value of α when its value is 1.1 can gen-
erate an error of more than 100% in the calculation of min-
imum number of trays. It can be imagined that the error in
the actual number of trays would be even higher than 100%.
In addition, the calculated numbers of trays are theoretical
and when converted to real number of trays through overall
column efficiency, the error may increase to several hundred
percent. The approach of building the column higher to have
a safe design is quite expensive.
As an example, a distillation column of diameter 4.5 m
% Deviation in Critical Temperature and height 85 m has an investment cost of approximately
$4 million (€4.5 million) as stated by Dohrn and Pfohl [60].
FIG. 1.5—Influence of error in critical temperature on errors
of predicted vapor pressure from Lee–Kesler method. Error in the calculation of relative volatility, α, could have
been caused by the error in calculation of vapor pressure,
which itself could have been caused by a small error in an
input parameter such as critical temperature [58, 59]. There-
properties and with other correlations for the estimation of fore, from this simple analysis one can realize the extreme
physical properties [59]. Effect of the error in the critical cost and loss in the investment that can be caused by a small
temperature on the vapor pressure of different compounds error in the estimation of critical temperature. Similar other
predicted from the Lee–Kesler method (see Section 7.3.2) is examples have been given in the literature [62]. Nowadays,
shown in Fig. 1.5. When the actual critical temperature is investment in refineries or their upgrading costs billions of
used, the error in the predicted vapor pressure is almost neg- dollars. For example, for a typical refinery of 160 000 bbl/d
ligible; however, if the critical temperature is under-predicted (8 million tons/year) capacity, the cost of construction in
by 5%, the error in the vapor pressure increases by 60–80% Europe is about $2 billion [18]. This is equivalent to refining
for the various compounds evaluated. cost of $7.5/bbl while this number for refineries of 1980s
As shown in Chapter 6, vapor pressure is one of the key was about $2/bbl. In addition to the extra cost of investment,
parameters in the calculation of equilibrium ratios (K i ) and inappropriate design of units can cause extra operating costs
subsequent relative volatility (α 12 ), which is defined in a bi- and shorten the plant life as well as produce products that
nary system of components 1 and 2 as follows: do not match the original design specifications. The use of a
proper characterization method to calculate more accurate
y 1
(1.3) K 1 =
x 1
K 1 y 1 x 2
(1.4) α 12 = = ×
K 2 x 1 y 2
where x 1 and x 2 are the mole fractions of components 1 and
2 in the liquid phase, respectively. Similarly y 1 and y 2 are the
mole fractions in the vapor phase for components 1 and 2,
respectively. For an ideal binary system at low pressure, the
equilibrium ratio K i is directly proportional to the vapor pres- % Error in Minimum Number of Plates
sure as will be seen in Chapter 6.
The most important aspect in the design and operation of
distillation columns is the number or trays needed to make a
specific separation for specific feed and products. It has been
shown that a small error in the value of relative volatility could
lead to a much greater error in the calculation of number of
trays and the length of a distillation column [60]. The mini-
mum number of trays required in a distillation column can be
calculated from the knowledge of relative volatility through % Error in Relative Volatility
the Fenske Equation given below [61].
FIG. 1.6—Effect of error in the relative volatil-
ln[x D (1 − x B )/x B (1 − x D )] ity on the error of minimum number of plates
(1.5) N min = − 1
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
ln(α 12 ) of a distillation column.
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT