Page 259 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
P2: KVU/KXT
QC: —/—
P1: KVU/KXT
20:46
June 22, 2007
AT029-Manual-v7.cls
AT029-Manual
AT029-06
6. THERMODYNAMIC RELATIONS FOR PROPERTY ESTIMATIONS 239
in some cases give negative heat capacities. Cubic equations
are widely used for calculation of molar volume (or density) 6 Liquid
and fugacity coefficients. Usually BWR or its various modi- 5 T r = 0.6
fied versions are used to calculate enthalpy and heat capacity.
The Lee–Kesler (LK) modification of BWR EOS is given by 4 0.8 --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Eq. (5.109). Upon use of this PVT relation, residual proper-
ties can be calculated. For example, by substituting Z from -[H-H ig ] (0) /RT c 3 Two-Phase 1
Region
Eq. (5.109) into Eqs. (6.53) and (6.36) the relations for the 1.5
fugacity coefficient and enthalpy departure are obtained and 2 Gas
are given by the following equations [9]: 0.8
2
1
f B C D

(6.54) ln = Z − 1 − ln(Z) + + + + E Vapor 4
P 2V 2 5V 5
V r
r r 0
0.01 0.1 1 10
H − H ig b 2 + 2b 3 /T r + 3b 4 /T r 2 Reduced Pressure, P r
= T r Z − 1 −
RT c T r V r (a)
c 2 − 3c 3 /T r 2 d 2
(6.55) − − + 3E 8
2T r V r 2 5T r V r 5
7 T r = 0.6
where parameter E in these equations is given by: Liquid
6

c 4 γ γ 5 0.8
E = 3 β + 1 − β + 1 + 2 exp − 2
2T γ V r V r 4
r
The coefficients in the above equations for the simple fluid -[H- H ig ] (1) /RTc 3 1
and reference fluid of n-octane are given in Table 5.8. Sim- 2
ig
ig
ilar equations for estimation of (C P − C ), (C V − C ), and Vapor Gas
V
P
ig
(S − S ) are given by Lee and Kesler [9]. To make use of these 1 0.6 1.5
equations for calculation of properties of all fluids a similar 0 2
approach as used to calculate Z through Eq. (5.108) is rec- 4
ommended. For practical calculations Eq. (6.55) and other -1
equations for fugacity and heat capacity can be converted 0.01 0.1 1 10
into the following corresponding states correlations:
Reduced Pressure, P r
H − H H − H H − H (b)
ig ig (0) ig (1)
(6.56) = + ω
RT c RT c RT c ig
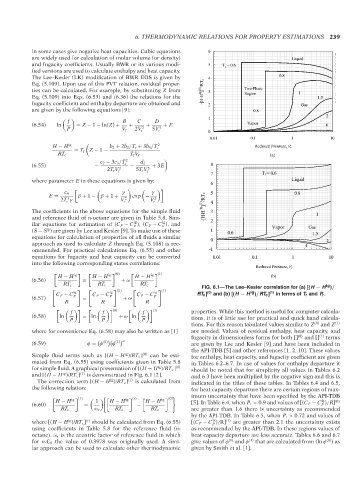
FIG. 6.1—The Lee–Kesler correlation for (a) [(H − H )/

(0)
(1)
ig
ig ig (0) ig (1)
C P − C C P − C C P − C RT c ] and (b) [(H − H )/RT c ] in terms of T r and P r .
(6.57) P = P + ω P
R R R
(0) (1)
f f f properties. While this method is useful for computer calcula-

(6.58) ln = ln + ω ln tions, it is of little use for practical and quick hand calcula-
P P P
tions. For this reason tabulated values similar to Z (0) and Z (1)
where for convenience Eq. (6.58) may also be written as [1] are needed. Values of residual enthalpy, heat capacity, and
fugacity in dimensionless forms for both [] (0) and [] (1) terms
(6.59) φ = φ (0) φ (1) ω are given by Lee and Kesler [9] and have been included in

the API-TDB [5] and other references [1, 2, 10]. These values
ig
Simple fluid terms such as [(H − H )/RT c ] (0) can be esti- for enthalpy, heat capacity, and fugacity coefficient are given
mated from Eq. (6.55) using coefficients given in Table 5.8 in Tables 6.2–6.7. In use of values for enthalpy departure it
ig
for simple fluid. A graphical presentation of [(H − H )/RT c ] (0) should be noted that for simplicity all values in Tables 6.2
ig
and [(H − H )/RT c ] (1) is demonstrated in Fig. 6.1 [2]. and 6.3 have been multiplied by the negative sign and this is
ig
The correction term [(H − H )/RT c ] (1) is calculated from indicated in the titles of these tables. In Tables 6.4 and 6.5,
the following relation: for heat capacity departure there are certain regions of max-
imum uncertainty that have been specified by the API-TDB

H − H 1 H − H H − H [5]. In Table 6.4, when P r > 0.9 and values of [(C P − C )/R] (0)
ig (1) ig (r) ig (0) ig
(6.60) = − P
RT c ω r RT c RT c are greater than 1.6 there is uncertainty as recommended
by the API-TDB. In Table 6.5, when P r > 0.72 and values of
ig
ig
where [(H − H )/RT c ] (r) should be calculated from Eq. (6.55) [(C P − C )/R] (1) are greater than 2.1 the uncertainty exists
P
using coefficients in Table 5.8 for the reference fluid (n- as recommended by the API-TDB. In these regions values of
octane). ω r is the acentric factor of reference fluid in which heat capacity departure are less accurate. Tables 6.6 and 6.7
(0)
for n-C 8 the value of 0.3978 was originally used. A simi- give values of φ (0) and φ (1) that are calculated from (ln φ )as
lar approach can be used to calculate other thermodynamic given by Smith et al. [1].
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT