Page 210 - Mechanical Behavior of Materials

Section 5.3 Elastic Deformation 211

x avg
P, Force

x
e ΔU

0
x, Distance

ΔU

Δx Δx
2 2

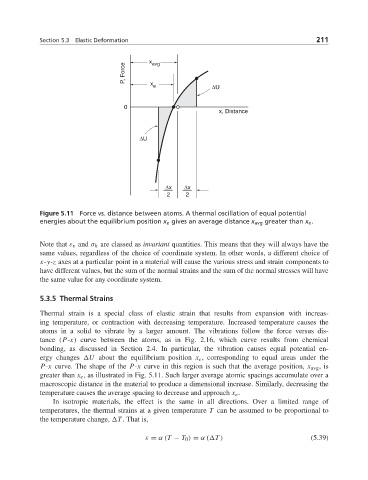
Figure 5.11 Force vs. distance between atoms. A thermal oscillation of equal potential
energies about the equilibrium position x e gives an average distance x avg greater than x e .

Note that ε v and σ h areclassedas invariant quantities. This means that they will always have the
same values, regardless of the choice of coordinate system. In other words, a different choice of
x-y-z axes at a particular point in a material will cause the various stress and strain components to
have different values, but the sum of the normal strains and the sum of the normal stresses will have
the same value for any coordinate system.

5.3.5 Thermal Strains

Thermal strain is a special class of elastic strain that results from expansion with increas-
ing temperature, or contraction with decreasing temperature. Increased temperature causes the
atoms in a solid to vibrate by a larger amount. The vibrations follow the force versus dis-
tance (P-x) curve between the atoms, as in Fig. 2.16, which curve results from chemical
bonding, as discussed in Section 2.4. In particular, the vibration causes equal potential en-
ergy changes U about the equilibrium position x e , corresponding to equal areas under the
P-x curve. The shape of the P-x curve in this region is such that the average position, x avg ,is
greater than x e , as illustrated in Fig. 5.11. Such larger average atomic spacings accumulate over a
macroscopic distance in the material to produce a dimensional increase. Similarly, decreasing the
temperature causes the average spacing to decrease and approach x e .
In isotropic materials, the effect is the same in all directions. Over a limited range of
temperatures, the thermal strains at a given temperature T can be assumed to be proportional to
the temperature change, T . That is,

ε = α (T − T 0 ) = α ( T ) (5.39)