Page 211 - Mechanical Behavior of Materials

212 Chapter 5 Stress–Strain Relationships and Behavior

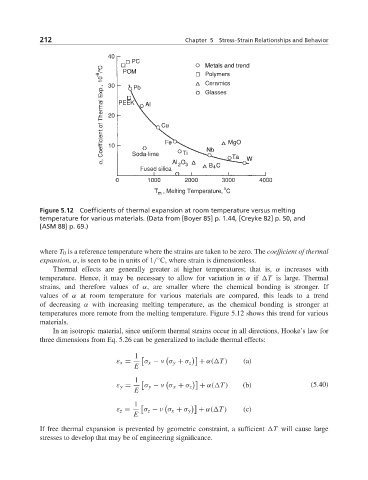
Figure 5.12 Coefficients of thermal expansion at room temperature versus melting
temperature for various materials. (Data from [Boyer 85] p. 1.44, [Creyke 82] p. 50, and
[ASM 88] p. 69.)

where T 0 is a reference temperature where the strains are taken to be zero. The coefficient of thermal
◦
expansion, α, is seen to be in units of 1/ C, where strain is dimensionless.
Thermal effects are generally greater at higher temperatures; that is, α increases with
temperature. Hence, it may be necessary to allow for variation in α if T is large. Thermal
strains, and therefore values of α, are smaller where the chemical bonding is stronger. If
values of α at room temperature for various materials are compared, this leads to a trend
of decreasing α with increasing melting temperature, as the chemical bonding is stronger at
temperatures more remote from the melting temperature. Figure 5.12 shows this trend for various
materials.
In an isotropic material, since uniform thermal strains occur in all directions, Hooke’s law for
three dimensions from Eq. 5.26 can be generalized to include thermal effects:

1
ε x = σ x − ν σ y + σ z + α( T ) (a)
E
1
ε y = σ y − ν σ x + σ z + α( T ) (b) (5.40)
E
1
ε z = σ z − ν σ x + σ y + α( T ) (c)
E
If free thermal expansion is prevented by geometric constraint, a sufficient T will cause large
stresses to develop that may be of engineering significance.