Page 212 - Mechanical Behavior of Materials

Section 5.3 Elastic Deformation 213

For example, consider the case of a smooth piece of material at temperature T i that is suddenly
immersed in a liquid or gas having a temperature T f . A thin surface layer will reach T f quickly, but
strain in the (x-y) plane of the surface will be prevented due to the material below not having had
time to adjust its temperature. Hence, we have ε x = ε y = 0, and also σ z = 0 due to the free surface.
Applying this situation to Eqs. 5.40(a) and (b) gives
Eα( T )
σ x = σ y =− (5.41)
1 − ν
where T = T f − T i , so that the stresses are compressive for a temperature increase, and tensile
for a decrease.

5.3.6 Comparison with Plastic and Creep Deformations

Elastic deformation, which is the stretching of chemical bonds, usually involves volume change, as
reflected in a Poisson’s ratio less than 0.5. However, plastic deformation and creep deformation
involve atoms changing neighbors by various mechanisms and so do not ordinarily result in
significant volume change. Consider the two-dimensional schematic of plastic deformation in
Fig. 2.19. The areas (a) before and (d) after slip are the same, implying constant volume. Similarly,
the movement of vacancies in creep does not cause volume change. (See Fig. 2.26.)
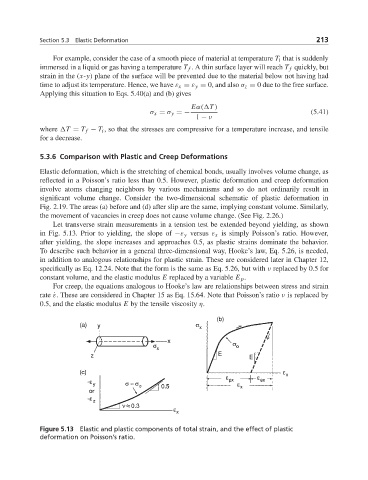
Let transverse strain measurements in a tension test be extended beyond yielding, as shown
in Fig. 5.13. Prior to yielding, the slope of −ε y versus ε x is simply Poisson’s ratio. However,
after yielding, the slope increases and approaches 0.5, as plastic strains dominate the behavior.
To describe such behavior in a general three-dimensional way, Hooke’s law, Eq. 5.26, is needed,
in addition to analogous relationships for plastic strain. These are considered later in Chapter 12,
specifically as Eq. 12.24. Note that the form is the same as Eq. 5.26, but with ν replaced by 0.5 for
constant volume, and the elastic modulus E replaced by a variable E p .
For creep, the equations analogous to Hooke’s law are relationships between stress and strain
rate ˙ε. These are considered in Chapter 15 as Eq. 15.64. Note that Poisson’s ratio ν is replaced by
0.5, and the elastic modulus E by the tensile viscosity η.

Figure 5.13 Elastic and plastic components of total strain, and the effect of plastic
deformation on Poisson’s ratio.