Page 119 - Introduction to Statistical Pattern Recognition

3 Hypothesis Testing 101

2 .o 1 .o

0 .a
- 0.6 9
on
t
w
1 .o
0.4

0.2

I
0.0 0.2 0.4 0.5 0.6 0.8 1.0
So =O .58
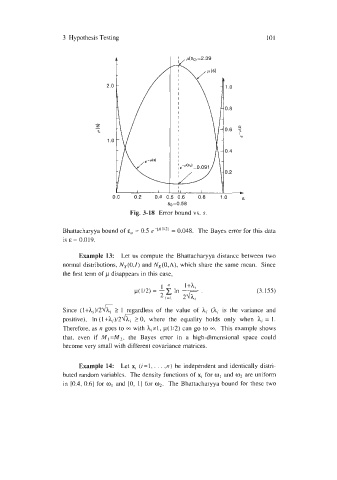
Fig. 3-18 Error bound vs. s.

Bhattacharyya bound of E, = 0.5 = 0.048. The Bayes error for this data
is E = 0.019.

Example 13: Let us compute the Bhattacharyya distance between two
normal distributions, Nx(O,I) and N,(O,A), which share the same mean. Since
the first term of J.I disappears in this case,

(3.155)

Since (1+Li)/2c 2 1 regardless of the value of h, (h, is the variance and
positive), In (l+h,)/2q 2 0, where the equality holds only when h, = 1.
Therefore, as n goes to 00 with L,#l, ~(112) can go to -. This example shows
that, even if M,=M2, the Bayes error in a high-dimensional space could
become very small with different covariance matrices.

Example 14: Let x, (i=l,. . . ,n) be independent and identically distri-
buted random variables. The density functions of xi for o1 and 02 are uniform
in [0.4, 0.61 for ol and [0, 11 for w2. The Bhattacharyya bound for these two