Page 21 - Introduction to Statistical Pattern Recognition

1 Introduction 3

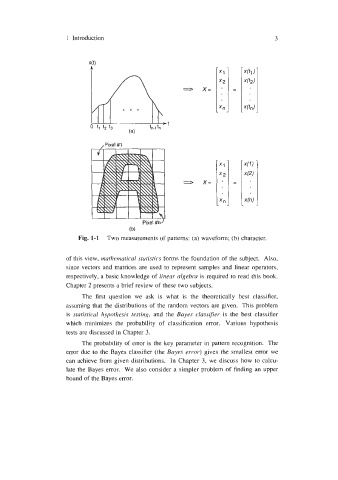
,Pixel #1

(b)
Fig. 1-1 Two measurements of patterns: (a) waveform; (b) character.

of this view, mathematical statistics forms the foundation of the subject. Also,
since vectors and matrices are used to represent samples and linear operators,
respectively, a basic knowledge of linear algebra is required to read this book.
Chapter 2 presents a brief review of these two subjects.

The first question we ask is what is the theoretically best classifier,
assuming that the distributions of the random vectors are given. This problem
is statistical hypothesis testing, and the Bayes classifier is the best classifier
which minimizes the probability of classification error. Various hypothesis
tests are discussed in Chapter 3.
The probability of error is the key parameter in pattern recognition. The
error due to the Bayes classifier (the Bayes error) gives the smallest error we
can achieve from given distributions. In Chapter 3, we discuss how to calcu-
late the Bayes error. We also consider a simpler problem of finding an upper
bound of the Bayes error.