Page 22 - Introduction to Statistical Pattern Recognition

4 Introduction to Statistical Pattern Recognition

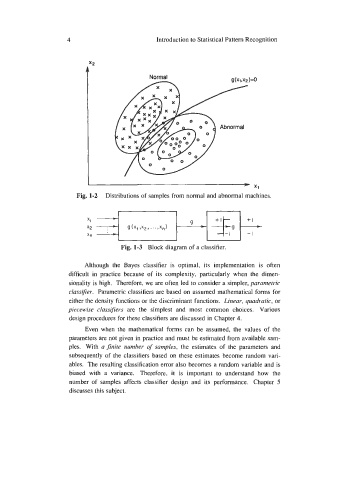
Fig. 1-2 Distributions of samples from normal and abnormal machines.

Although the Bayes classifier is optimal, its implementation is often
difficult in practice because of its complexity, particularly when the dimen-
sionality is high. Therefore, we are often led to consider a simpler, parametric
classifier. Parametric classifiers are based on assumed mathematical forms for
either the density functions or the discriminant functions. Linear, quadratic, or
piecewise classifiers are the simplest and most common choices. Various
design procedures for these classifiers are discussed in Chapter 4.
Even when the mathematical forms can be assumed, the values of the
parameters are not given in practice and must be estimated from available sam-
ples. With a finite number of samples, the estimates of the parameters and
subsequently of the classifiers based on these estimates become random vari-
ables. The resulting classification error also becomes a random variable and is
biased with a variance. Therefore, it is important to understand how the
number of samples affects classifier design and its performance. Chapter 5
discusses this subject.