Page 230 - Introduction to Statistical Pattern Recognition

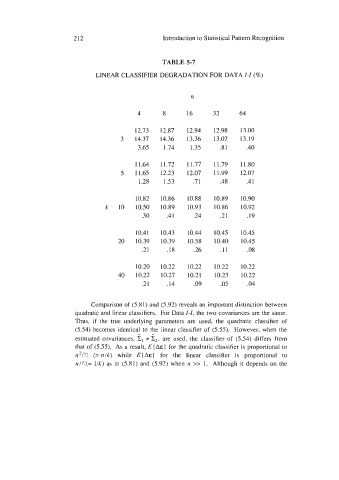
212 Introduction to Statistical Pattern Recognition

TABLE 5-7

LINEAR CLASSIFIER DEGRADATION FOR DATA I-I (%)

n

4 8 16 32 64

12.73 12.87 12.94 12.98 13.00
3 14.37 14.36 13.36 13.02 13.19
3.65 1.74 1.35 .8 1 .40

11.64 11.72 11.77 1 1.79 1.80
5 11.65 12.23 12.07 11.99 2.07
1.28 1.53 .7 1 .48 .4 1

10.82 10.86 10.88 10.89 0.90
k 10 10.50 10.89 10.93 10.86 10.92
.30 .4 1 -24 .2 1 .I9

10.4 1 10.43 10.44 10.45 10.45
20 10.39 10.39 10.58 10.40 10.45
.21 .18 .26 .11 .08

10.20 10.22 10.22 10.22 10.22
40 10.22 10.27 10.21 10.23 10.22
.2 1 .I4 .09 .05 -04

Comparison of (5.8 1) and (5.92) reveals an important distinction between
quadratic and linear classifiers. For Data 1-1, the two covariances are the same.
Thus, if the true underlying parameters are used, the quadratic classifier of
(5.54) becomes identical to the linear classifier of (5.55). However, when the
a n
estimated covariances, I:, f Cz, are used, the classifier of (5.54) differs from
that of (5.55). As a result, E (A& 1 for the quadratic classifier is proportional to
n2/n (= nlk) while E{Aa) for the linear classifier is proportional to
nl?I(= Ilk) as in (5.81) and (5.92) when n >> 1. Although it depends on the