Page 298 - Introduction to Statistical Pattern Recognition

280 Introduction to Statistical Pattern Recognition

experimental result
- 1st order approx.
~NN
ONN
10 0.5

8 0.4

6 0.3

4 0.2

2 0.1

0 0.0
1 2 3 4 5 6
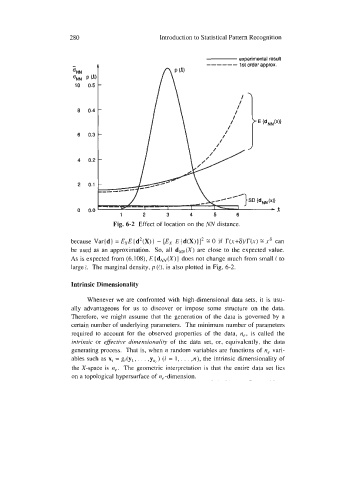
Fig. 6-2 Effect of location on the NN distance.

because Var(d) =ExE(d2(X)) - [E, E(d(X))I2 EO if T(x+6)/T(x) Ex6 can
be used as an approximation. So, all dNN(X) are close to the expected value.
As is expected from (6.108), E ( dNN(X)) does not change much from small S to
large e. The marginal density, p (t), is also plotted in Fig. 6-2.

Intrinsic Dimensionality

Whenever we are confronted with high-dimensional data sets, it is usu-
ally advantageous for us to discover or impose some structure on the data.
Therefore, we might assume that the generation of the data is governed by a
certain number of underlying parameters. The minimum number of parameters
required to account for the observed properties of the data, n,, is called the
intrinsic or effective dimensionality of the data set, or, equivalently, the data
generating process. That is, when n random variables are functions of ne vari-
ables such as xi = gi(yl, . . . ,y,J (i = 1, . . . ,n), the intrinsic dimensionality of
the X-space is n,. The geometric interpretation is that the entire data set lies
on a topological hypersurface of n,-dimension.