Page 336 - Introduction to Statistical Pattern Recognition

318 Introduction to Statistical Pattern Recognition

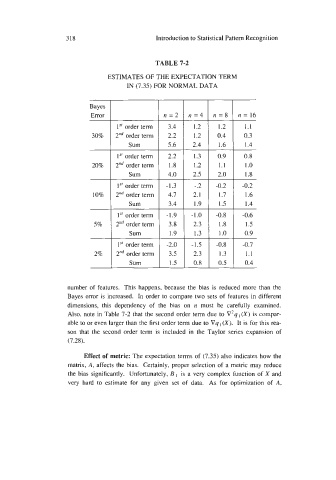
TABLE 7-2

ESTIMATES OF THE EXPECTATION TERM
IN (7.35) FOR NORMAL DATA

Bayes
Error n = 16
1'' order term 3.4 1.1
30% 2"d order term 2.2 0.3
Sum 5.6 1.4
1'' order term 2.2 1.3 0.9 0.8
20% 2"d order term 1.8 1.2 1.1 1 .o
Sum 4.0 2.5 2.0 1.8
1'' order term -1.3 -0.2
10% 2'ld order term 4.7 1.6
Sum 3.4 1.4
1'' order term -1.9 -0.6
5% 2"d order term 3.8 1.5
Sum 1.9 0.9
1" order term -2.0 -1.5 -0.8 -0.7
2% 2'ld order term 3.5 2.3 1.1
Sum 1.5 0.8 0.5 0.4

number of features. This happens, because the bias is reduced more than the
Bayes error is increased. In order to compare two sets of features in different
dimensions, this dependency of the bias on n must be carefully examined.
Also, note in Table 7-2 that the second order term due to V2q,(X) is compar-
able to or even larger than the first order term due to Vq I (X). It is for this rea-
son that the second order term is included in the Taylor series expansion of
(7.28).
Effect of metric: The expectation terms of (7.35) also indicates how the
matrix, A, affects the bias. Certainly, proper selection of a metric may reduce
the bias significantly. Unfortunately, BI is a very complex function of X and
very hard to estimate for any given set of data. As for optimization of A,