Page 378 - Introduction to Statistical Pattern Recognition

360 Introduction to Statistical Pattern Recognition

r
4

No Editing- /

I //

0 .05 .IO .I 5 .20 .25
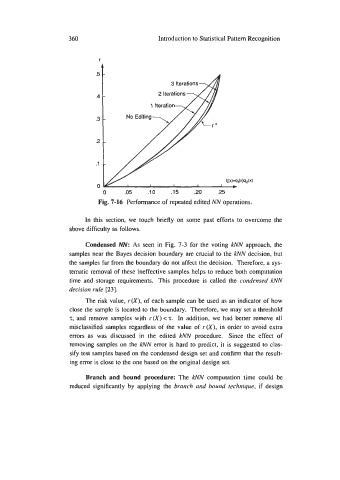
Fig. 7-16 Performance of repeated edited NN operations.

In this section, we touch briefly on some past efforts to overcome the
above difficulty as follows.

Condensed NN: As seen in Fig. 7-3 for the voting kNN approach, the
samples near the Bayes decision boundary are crucial to the kNN decision, but
the samples far from the boundary do not affect the decision. Therefore, a sys-
tematic removal of these ineffective samples helps to reduce both computation
time and storage requirements. This procedure is called the condensed kNN
decision rule [23].
The risk value, r(X), of each sample can be used as an indicator of how
close the sample is located to the boundary. Therefore, we may set a threshold
z, and remove samples with I' (X) < z. In addition, we had better remove all
misclassified samples regardless of the value of r(X), in order to avoid extra
errors as was discussed in the edited kNN procedure. Since the effect of
removing samples on the kNN error is hard to predict, it is suggested to clas-
sify test samples based on the condensed design set and confirm that the result-
ing error is close to the one based on the original design set.

Branch and bound procedure: The kNN computation time could be
reduced significantly by applying the brunch and bound technique, if design