Page 121 - A Practical Companion to Reservoir Stimulation

PRACTICAL COMPANION TO RESERVOIR STIMULATION

EXAMPLE G-8 EXAMPLE G-9

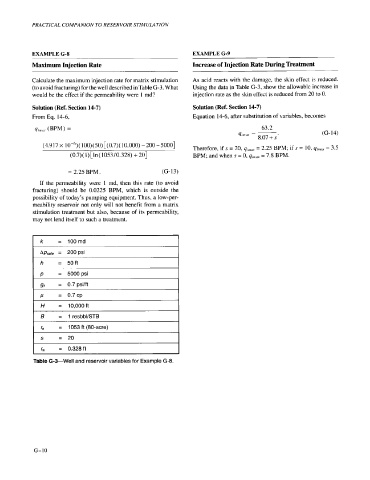
Maximum Injection Rate Increase of Injection Rate During Treatment

Calculate the maximum injection rate for matrix stimulation As acid reacts with the damage, the skin effect is reduced.
(to avoid fracturing) for the well described in Table G-3. What Using the data in Table (3-3, show the allowable increase in
would be the effect if the permeability were 1 md? injection rate as the skin effect is reduced from 20 to 0.
Solution (Ref. Section 14-7) Solution (Ref. Section 14-7)
From Eq. 14-6, Equation 14-6, after substitution of variables, becomes

qiniut (BPM) = 63.2
qlnl'n = ((3-14)
8.07 + s
(4.917 x lo-')( 100)(50)[(0.7)( l0,OOO) -200-5000] Therefore, if s = 20, qirinrr = 2.25 BPM; if s = 10, q;nl,,.r = 3.5
(0.7)( l)[ln( 1053/0.328) + 201 BPM; and when s = 0, qiIllnx = 7.8 BPM.

= 2.25 BPM . (G- 13)

If the permeability were 1 md, then this rate (to avoid
fracturing) should be 0.0225 BPM, which is outside the
possibility of today's pumping equipment. Thus, a low-per-
meability reservoir not only will not benefit from a matrix
stimulation treatment but also, because of its permeability,
may not lend itself to such a treatment.

Ik = l00md
~~~~~~ ~ ~
Apsafe = 200 psi
h = 50ft
pk--
I
P
= 5000psi
= 0.7 psilft
I gf

= 1 resbbl/STB

I re = 1053 ft (80-acre)
I s = 20
1, = 0.328ft

Table G-3-Well and reservoir variables for Example G-8.