Page 219 - A Practical Introduction to Optical Mineralogy

REFLECTED-LIGHT THEORY
interested reader is referred to the textbook by Galopin and Henry
;>-.
....
(1972). v
Returning to the Fresnel equation, it is worth noting that this equation ~E
"'
explains why opaque minerals appear 'bright' in polished section. OE .::2 c
V>;>-.
" "'
C-
Although the reflectance of a transparent mineral increases with refrac- roro u
- o.-- u "
tive index, a small increase in the absorption coefficient (i.e. opacity) "'
o O..
leads to a marked increase in reflectance. c o
Examples of the relationship between refractive index, absorption
coefficient and reflectance are shown for a range of minerals in Table
1.1. These examples emphasise the continuity in optical properties from
transparent minerals, through weakly absorbing minerals, to truly
opaque minerals.
"'
:§
-g
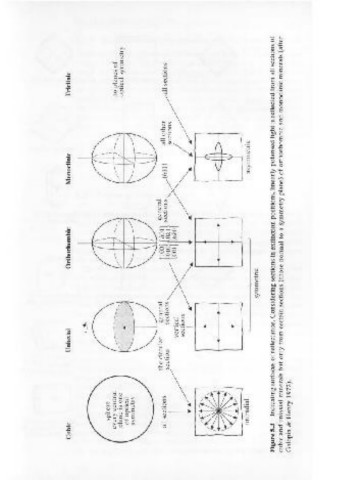
5.1.2 Indicating surfaces of reflectance =
0
::;
As outlined above, the reflectance of minerals varies with crystallo-
graphic orientation. The directional nature of the reflectance can be
described using an indicating surface which is analogous to but not ~=
~ .Q
identical with the refractive index indicatrix. The geometrical relation- c~
ship between indicating surfaces and crystal symmetry is illustrated in
Figure 5.3. The simplest surface is that for the cubic system; there is no ""'O""' ~ -EE
"' :.0 0->(-'<:
variation in reflectance with orientation, so the indicating surface is a E - ---{'-----t---"'1-.,.-+--- ----'01 =----+
..
0
sphere. The surface for uniaxial minerals is a surface of rotation about ..c oo-=-
o-o
0 -oo
..
the c axis; there is usually only a slight departure from a truly ellipsoidal -5 ~
surface. There is no theoretically correct surface for lower symmetry 0
minerals because only certain crystallographic orientations reflect · ~
linearly polarised light. "
E
E
~
5.1.3 Observing the effects of crystallographic orientation on
reflectance
.... u
We are now in a position to understand reflection of light from aggre- .... ""
>"'
gates of grains of a mineral as observed · using plane polarised light. "' :;
u c
Cubic minerals have one reflectance value and one colour; there is no =
0 -
u-
variation from grain to grain or within one grain on rotating the stage. o.> U
_c O)
Uniaxial minerals may vary in appearance from grain to grain; on
rotation of the stage it should be possible at some position to make two
grains of differing orientation appear identical in brightness and colour.
Sections normal to the c axis of uniaxial minerals do not vary on rotation
of the stage. Most grains of lower symmetry minerals will vary in
"
u-4 "'
reflectance and perhaps colour on rotating the stage. ~ · ~
....
Although it is easy to explain the behaviour of a mineral in terms of its "' :.0 = =
"'
=
crystal symmetry it is certainly not easy, and in any case usually unneces- u
sary, to determine crystal symmetry from polished sections of minerals.
See Figure 5.4, where the symmetry of crystals is illustrated.
206