Page 217 - A Practical Introduction to Optical Mineralogy

REFLECTED-LIGHT THEORY

where, for a wavelength value (A.), R % is the percentage reflectance, n is
a refractive index of the mineral, k is an absorption coefficient of the
mineral and N is the refractive index of the immersion medium.
The equation is strictly for reflection of linearly polarised light under
normal incidence. It simplifies for observations in air where N = 1 for all
wavelengths and for transparent minerals where k = 0.
The dispersion of the optical properties (i.e. their variation with
wavelength) is much more important in understanding minerals in
reflected light than in transmitted light.
The refractive index (n) and its variation with crystallographic orien-
tation is dealt with in the theory of optical mineralogy for transmitted
light studies (Section 4.2). However, it is worth noting that opaque
minerals also have a refractive index.
The absorption coefficient (k) is a measure of opacity. As light of a
given wavelength passes through matter it is progressively absorbed and
the decrease in intensity is related to the absorption coefficient in the
equation:
A = Aoe - hkdl~>.,

where A 0 is the initial amplitude of a wave of wavelength A. 0 , A is the
amplitude after traversing a distanced in the crystal and e is the base of
natural logarithms.
The intensity of a light wave is the square of the amplitude:

I = A 2
2.5~ , ---;
--
A mineral will appear opaque in thin section (0.03 mm thick) if its n 2.3 ------~------~-------~
absorption coefficient is 0.01 or greater. The absorption coefficient
varies with crystallographic orientation in the same way as the refractive 2. 1-1 I I I I
index. Thus, for cubic minerals there is one refractive index (n) and one
absorption coefficient (k); for uniaxial minerals the appropriate symbols
are n 0 =f n 0 and k 0 i- k.; and for lower symmetry minerals n. < n ~ < n , k ,::k:=:---~'~-====
and k . < k p < k ,.
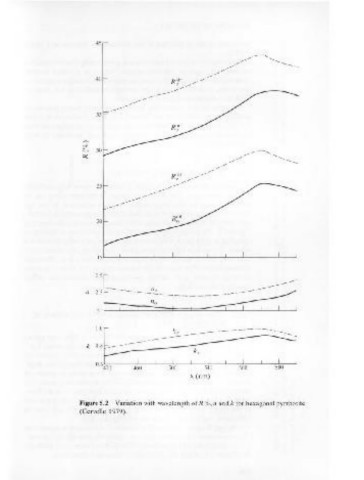
The relationship between the optical constants and reflectance and
the variation with wavelength is shown using hexagonal pyrrhotite as an 0 6
540
example in Figure 5.2. Remembering that the Fresnel equation holds at · 420 460 500 ), (nm) 560 580
each wavelength, it can be seen how the spectral reflectance curves of
pyrrhotite are related to the dispersion curves of the optical constants. It
is because ofthe variation ofreflectance with wavelength that pyrrhotite
Figure 5.2 Variation with wavelength of R %, n and k for hexagonal pyrrhotite
appears slightly coloured in polished section. More will be said on the
(Cervelle 1979).
colour of minerals in reflected light later.
Although an understanding of spectral reflectance curves is useful in
the qualitative examination of minerals in polished section, a thorough
treatment of theoretical aspects of reflected light and the measurement
of reflectance and optical constants is unnecessary at this level, and the
204