Page 391 - Acquisition and Processing of Marine Seismic Data

382 7. SUPPRESSION OF MULTIPLE REFLECTIONS

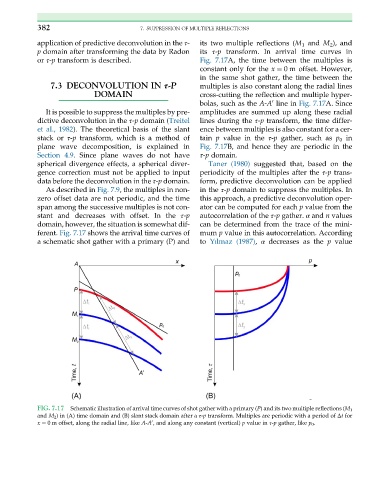
application of predictive deconvolution in the τ- its two multiple reflections (M 1 and M 2 ), and
p domain after transforming the data by Radon its τ-p transform. In arrival time curves in
or τ-p transform is described. Fig. 7.17A, the time between the multiples is
constant only for the x ¼ 0 m offset. However,
in the same shot gather, the time between the
7.3 DECONVOLUTION IN τ-P multiples is also constant along the radial lines
DOMAIN cross-cutting the reflection and multiple hyper-
bolas, such as the A-A line in Fig. 7.17A. Since
0
It is possible to suppress the multiples by pre- amplitudes are summed up along these radial
dictive deconvolution in the τ-p domain (Treitel lines during the τ-p transform, the time differ-
et al., 1982). The theoretical basis of the slant ence between multiples is also constant for a cer-
stack or τ-p transform, which is a method of tain p value in the τ-p gather, such as p 0 in
plane wave decomposition, is explained in Fig. 7.17B, and hence they are periodic in the
Section 4.9. Since plane waves do not have τ-p domain.
spherical divergence effects, a spherical diver- Taner (1980) suggested that, based on the
gence correction must not be applied to input periodicity of the multiples after the τ-p trans-
data before the deconvolution in the τ-p domain. form, predictive deconvolution can be applied
As described in Fig. 7.9, the multiples in non- in the τ-p domain to suppress the multiples. In
zero offset data are not periodic, and the time this approach, a predictive deconvolution oper-
span among the successive multiples is not con- ator can be computed for each p value from the
stant and decreases with offset. In the τ-p autocorrelation of the τ-p gather. α and n values
domain, however, the situation is somewhat dif- can be determined from the trace of the mini-
ferent. Fig. 7.17 shows the arrival time curves of mum p value in this autocorrelation. According
a schematic shot gather with a primary (P) and to Yılmaz (1987), α decreases as the p value

FIG. 7.17 Schematic illustration of arrival time curves of shot gather with a primary (P) and its two multiple reflections (M 1
and M 2 ) in (A) time domain and (B) slant stack domain after a τ-p transform. Multiples are periodic with a period of Δt for
x ¼ 0 m offset, along the radial line, like A-A , and along any constant (vertical) p value in τ-p gather, like p 0 .
0