Page 471 - Acquisition and Processing of Marine Seismic Data

462 10. NORMAL MOVEOUT CORRECTION AND STACKING

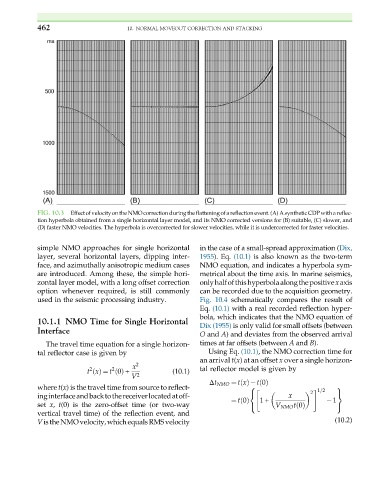
FIG. 10.3 EffectofvelocityontheNMOcorrectionduringtheflatteningofareflectionevent.(A) Asynthetic CDPwithareflec-
tion hyperbola obtained from a single horizontal layer model, and its NMO corrected versions for (B) suitable, (C) slower, and
(D) faster NMO velocities. The hyperbola is overcorrected for slower velocities, while it is undercorrected for faster velocities.

simple NMO approaches for single horizontal in the case of a small-spread approximation (Dix,
layer, several horizontal layers, dipping inter- 1955). Eq. (10.1) is also known as the two-term
face, and azimuthally anisotropic medium cases NMO equation, and indicates a hyperbola sym-
are introduced. Among these, the simple hori- metrical about the time axis. In marine seismics,
zontal layer model, with a long offset correction onlyhalfofthishyperbolaalongthepositivexaxis
option whenever required, is still commonly can be recorded due to the acquisition geometry.
used in the seismic processing industry. Fig. 10.4 schematically compares the result of
Eq. (10.1) with a real recorded reflection hyper-
bola, which indicates that the NMO equation of
10.1.1 NMO Time for Single Horizontal
Interface Dix (1955) is only valid for small offsets (between
O and A) and deviates from the observed arrival
The travel time equation for a single horizon- times at far offsets (between A and B).
tal reflector case is given by Using Eq. (10.1), the NMO correction time for
an arrival t(x) at an offset x over a single horizon-
x 2
2
2
t xðÞ ¼ t 0ðÞ + (10.1) tal reflector model is given by
V 2
Δt NMO ¼ txðÞ t 0ðÞ
where t(x) is the travel time from source to reflect- 8 9
" # 1=2
2 =
inginterfaceandbacktothereceiverlocatedatoff- x
<
¼ t 0ðÞ 1+ 1
set x, t(0) is the zero-offset time (or two-way : V NMO t 0ðÞ ;
vertical travel time) of the reflection event, and
VistheNMOvelocity,whichequalsRMSvelocity (10.2)