Page 111 - Adaptive Identification and Control of Uncertain Systems with Nonsmooth Dynamics

104 Adaptive Identification and Control of Uncertain Systems with Non-smooth Dynamics

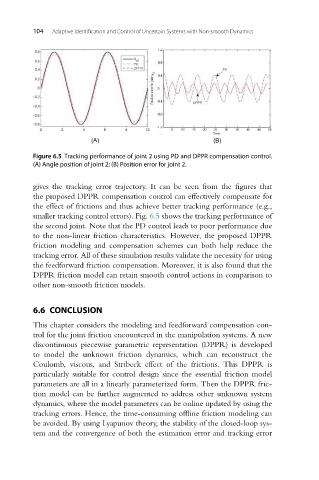
Figure 6.5 Tracking performance of joint 2 using PD and DPPR compensation control.
(A) Angle position of joint 2; (B) Position error for joint 2.

gives the tracking error trajectory. It can be seen from the figures that
the proposed DPPR compensation control can effectively compensate for
the effect of frictions and thus achieve better tracking performance (e.g.,
smaller tracking control errors). Fig. 6.5 shows the tracking performance of
the second joint. Note that the PD control leads to poor performance due
to the non-linear friction characteristics. However, the proposed DPPR
friction modeling and compensation schemes can both help reduce the
tracking error. All of these simulation results validate the necessity for using
the feedforward friction compensation. Moreover, it is also found that the
DPPR friction model can retain smooth control actions in comparison to
other non-smooth friction models.

6.6 CONCLUSION
This chapter considers the modeling and feedforward compensation con-
trol for the joint friction encountered in the manipulation systems. A new
discontinuous piecewise parametric representation (DPPR) is developed
to model the unknown friction dynamics, which can reconstruct the
Coulomb, viscous, and Stribeck effect of the frictions. This DPPR is
particularly suitable for control design since the essential friction model
parameters are all in a linearly parameterized form. Then the DPPR fric-
tion model can be further augmented to address other unknown system
dynamics, where the model parameters can be online updated by using the
tracking errors. Hence, the time-consuming offline friction modeling can
be avoided. By using Lyapunov theory, the stability of the closed-loop sys-
tem and the convergence of both the estimation error and tracking error