Page 296 - Adaptive Identification and Control of Uncertain Systems with Nonsmooth Dynamics

Adaptive Estimation and Control of Magneto-Rheological Damper for Semi-Active Suspensions 299

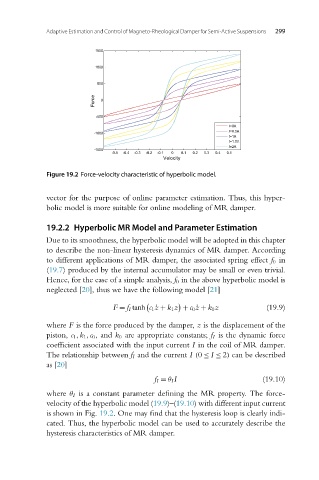
Figure 19.2 Force-velocity characteristic of hyperbolic model.

vector for the purpose of online parameter estimation. Thus, this hyper-
bolic model is more suitable for online modeling of MR damper.

19.2.2 Hyperbolic MR Model and Parameter Estimation
Due to its smoothness, the hyperbolic model will be adopted in this chapter
to describe the non-linear hysteresis dynamics of MR damper. According
to different applications of MR damper, the associated spring effect f 0 in
(19.7) produced by the internal accumulator may be small or even trivial.
Hence, for the ease of a simple analysis, f 0 in the above hyperbolic model is
neglected [20], thus we have the following model [21]

F = f I tanh c 1 ˙z + k 1z + c 0 ˙z + k 0z (19.9)

where F is the force produced by the damper, z is the displacement of the
piston, c 1 ,k 1 ,c 0,and k 0 are appropriate constants; f I is the dynamic force
coefficient associated with the input current I in the coil of MR damper.
The relationship between f I and the current I (0 ≤ I ≤ 2) can be described
as [20]

f I = θ I I (19.10)
where θ I is a constant parameter defining the MR property. The force-
velocity of the hyperbolic model (19.9)–(19.10) with different input current
isshowninFig. 19.2. One may find that the hysteresis loop is clearly indi-
cated. Thus, the hyperbolic model can be used to accurately describe the
hysteresis characteristics of MR damper.