Page 140 - Advanced Thermodynamics for Engineers, Second Edition

6.3 EFFICIENCY OF COMBINED CYCLE INTERNALLY REVERSIBLE HEAT 127

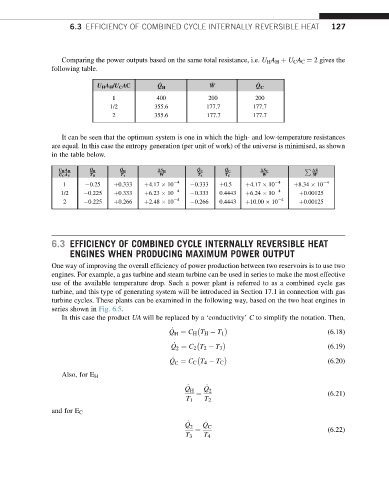
Comparing the power outputs based on the same total resistance, i.e. U H A H þ U C A C ¼ 2 gives the
following table.

_
_
U H A H /U C AC Q H _ W Q C
1 400 200 200
1/2 355.6 177.7 177.7
2 355.6 177.7 177.7

It can be seen that the optimum system is one in which the high- and low-temperature resistances
are equal. In this case the entropy generation (per unit of work) of the universe is minimised, as shown
in the table below.

P DS
U H A H _ Q H _ Q H DS H _ Q C _ Q C DS C
W W W
U C A C T H T 1 T 2 T C
1 0.25 þ0.333 þ4.17 10 4 0.333 þ0.5 þ4.17 10 4 þ8.34 10 4
1/2 0.225 þ0.333 þ6.23 10 4 0.333 0.4443 þ6.24 10 4 þ0.00125
2 0.225 þ0.266 þ2.48 10 4 0.266 0.4443 þ10.00 10 4 þ0.00125

6.3 EFFICIENCY OF COMBINED CYCLE INTERNALLY REVERSIBLE HEAT
ENGINES WHEN PRODUCING MAXIMUM POWER OUTPUT

One way of improving the overall efficiency of power production between two reservoirs is to use two
engines. For example, a gas turbine and steam turbine can be used in series to make the most effective
use of the available temperature drop. Such a power plant is referred to as a combined cycle gas
turbine, and this type of generating system will be introduced in Section 17.1 in connection with gas
turbine cycles. These plants can be examined in the following way, based on the two heat engines in
series shown in Fig. 6.5.
In this case the product UA will be replaced by a ‘conductivity’ C to simplify the notation. Then,

_
Q ¼ C H T H T 1 (6.18)
H
_
Q ¼ C 2 T 2 T 3 (6.19)
2
_
C
Q ¼ C C T 4 T C (6.20)
Also, for E H
Q _ H Q _ 2
¼ (6.21)
T 1 T 2
and for E C
Q _ Q _
2 C
¼ (6.22)
T 3 T 4