Page 101 - Advanced engineering mathematics

3.2 Solution of Initial Value Problems 81

3.2 Solution of Initial Value Problems

To apply the Laplace transform to the solution of an initial value problem, we must
be able to transform a derivative. This involves the concept of a piecewise continuous
function.

Suppose f (t) is defined at least on [a,b]. Then f is piecewise continuous on [a,b] if:
1. f is continuous at all but perhaps finitely many points of [a,b].
2. If f is not continuous at t 0 in (a,b), then f (t) has finite limits from both sides at t 0 .
3. f (t) has finite limits as t approaches a and as t approaches b from within the
interval.

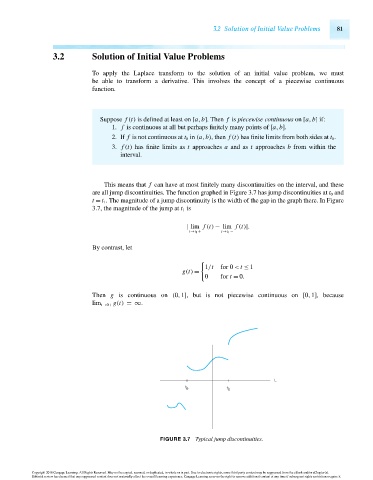
This means that f can have at most finitely many discontinuities on the interval, and these
are all jump discontinuities. The function graphed in Figure 3.7 has jump discontinuities at t 0 and
t =t 1 . The magnitude of a jump discontinuity is the width of the gap in the graph there. In Figure
3.7, the magnitude of the jump at t 1 is

| lim f (t) − lim f (t)|.
t→t 1 + t→t 1 −

By contrast, let

1/t for 0 < t ≤ 1
g(t) =
0 for t = 0.

Then g is continuous on (0,1], but is not piecewise continuous on [0,1], because
lim t→0+ g(t) =∞.

t
t 0 t 1

FIGURE 3.7 Typical jump discontinuities.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:14 THM/NEIL Page-81 27410_03_ch03_p77-120