Page 366 - Advanced engineering mathematics

346 CHAPTER 11 Vector Differential Calculus

100
80
–1
60
–0.5 40
20
0
0
20
0.5
40
1
60
80

100

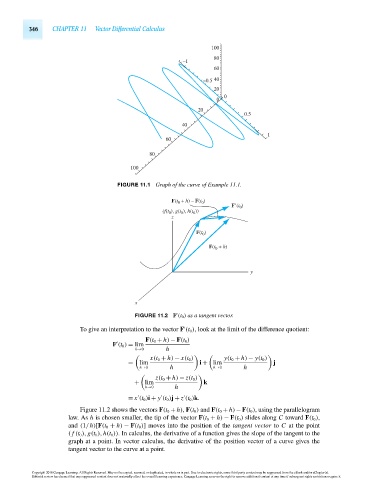
FIGURE 11.1 Graph of the curve of Example 11.1.

F(t + h) – F(t )
0
0
F (t )
0
(f(t ), g(t ), h(t ))
0
0
0
z
F(t )
0
F(t + h)
0
y

x
FIGURE 11.2 F (t 0 ) as a tangent vector.

To give an interpretation to the vector F (t 0 ), look at the limit of the difference quotient:

F(t 0 + h) − F(t 0 )
F (t 0 ) = lim

h→0 h

x(t 0 + h) − x(t 0 ) y(t 0 + h) − y(t 0 )
= lim i + lim j
h→0 h h→0 h

z(t 0 + h) − z(t 0 )
+ lim k
h→0 h

= x (t 0 )i + y (t 0 )j + z (t 0 )k.
Figure 11.2 shows the vectors F(t 0 + h), F(t 0 ) and F(t 0 + h)−F(t 0 ), using the parallelogram
law. As h is chosen smaller, the tip of the vector F(t 0 + h) − F(t 0 ) slides along C toward F(t 0 ),
and (1/h)[F(t 0 + h) − F(t 0 )] moves into the position of the tangent vector to C at the point
( f (t 0 ), g(t 0 ),h(t 0 )). In calculus, the derivative of a function gives the slope of the tangent to the
graph at a point. In vector calculus, the derivative of the position vector of a curve gives the
tangent vector to the curve at a point.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 15, 2010 16:11 THM/NEIL Page-346 27410_11_ch11_p343-366