Page 85 - Advanced thermodynamics for engineers

70 CHAPTER 4 AVAILABILITY AND EXERGY

Temperature, T b

dS
1
4 T 1 = T 4 = T

a

T 2 = T 0 d 3 2 c

e n m f
Entropy, S
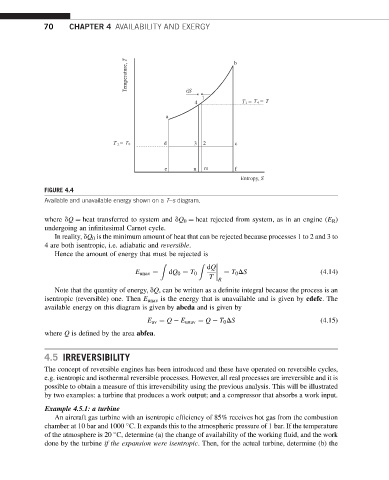
FIGURE 4.4
Available and unavailable energy shown on a T–s diagram.

where dQ ¼ heat transferred to system and dQ 0 ¼ heat rejected from system, as in an engine (E R )
undergoing an infinitesimal Carnot cycle.
In reality, dQ 0 is the minimum amount of heat that can be rejected because processes 1 to 2 and 3 to
4 are both isentropic, i.e. adiabatic and reversible.
Hence the amount of energy that must be rejected is

Z Z
dQ
E unav ¼ dQ 0 ¼ T 0 ¼ T 0 DS (4.14)
T R
Note that the quantity of energy, dQ, can be written as a definite integral because the process is an
isentropic (reversible) one. Then E unav is the energy that is unavailable and is given by cdefc. The
available energy on this diagram is given by abcda and is given by
E av ¼ Q E unav ¼ Q T 0 DS (4.15)
where Q is defined by the area abfea.

4.5 IRREVERSIBILITY
The concept of reversible engines has been introduced and these have operated on reversible cycles,
e.g. isentropic and isothermal reversible processes. However, all real processes are irreversible and it is
possible to obtain a measure of this irreversibility using the previous analysis. This will be illustrated
by two examples: a turbine that produces a work output; and a compressor that absorbs a work input.
Example 4.5.1: a turbine
An aircraft gas turbine with an isentropic efficiency of 85% receives hot gas from the combustion
chamber at 10 bar and 1000 C. It expands this to the atmospheric pressure of 1 bar. If the temperature

of the atmosphere is 20 C, determine (a) the change of availability of the working fluid, and the work

done by the turbine if the expansion were isentropic. Then, for the actual turbine, determine (b) the