Page 115 - Aerodynamics for Engineering Students

98 Aerodynamics for Engineering Students

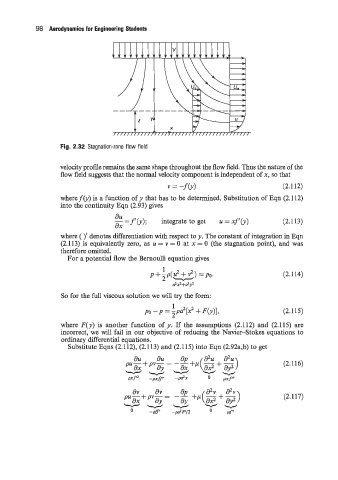
Fig. 2.32 Stagnation-zone flow field

velocity profile remains the same shape throughout the flow field. Thus the nature of the
flow field suggests that the normal velocity component is independent of x, so that
v = -f 0.1) (2.112)

where f(y) is a function of y that has to be determined. Substitution of Eqn (2.1 12)
into the continuity Eqn (2.93) gives
824
- =f'(y); integrate to get u = xf'(y) (2.113)
ax
where ( )' denotes differentiation with respect to y. The constant of integration in Eqn
(2.113) is equivalently zero, as u = v = 0 at x = 0 (the stagnation point), and was
therefore omitted.
For a potential flow the Bernoulli equation gives
1
P + p(+) =Po. (2.114)
dXz+$yZ
So for the full viscous solution we will try the form:

(2.1 1 5)
where F( y) is another function of y. If the assumptions (2.112) and (2.11 5) are
incorrect, we will fail in our objective of reducing the NavierStokes equations to
ordinary differential equations.
Substitute Eqns (2.112), (2.113) and (2.115) into Eqn (2.92a,b) to get

d2U
ap
au au = -- +p(- a2u + -) (2.116)
pu-++v-
ay
--- Ys
ax
ax
ay2
ax2
-w=x
-pxp
PXfR
av av
pu-++v-= (2.117)
ax ay
-P?' -@F'/2