Page 295 - Aerodynamics for Engineering Students

Compressible flow 277

Equation (6.12) indicates the way in which the cross-sectional area of the stream tube
must change to produce a change in velocity for a given mass flow. It will be noted
that a change of sign occurs at M = 1.
For subsonic flow dA must be negative for an increase, Le. a positive change, in
velocity. At M = 1, dA is zero and a throat appears in the tube. For acceleration to
supersonic flow a positive change in area is required, that is, the tube diverges from
the point of minimum cross-sectional area.
Eqn (6.12) indicates that a stream tube along which gas speeds up from subsonic to
supersonic velocity must have a converging-diverging shape. For the reverse process,
the one of slowing down, a similar change in tube area is theoretically required but
such a deceleration from supersonic flow is not possible in practice.
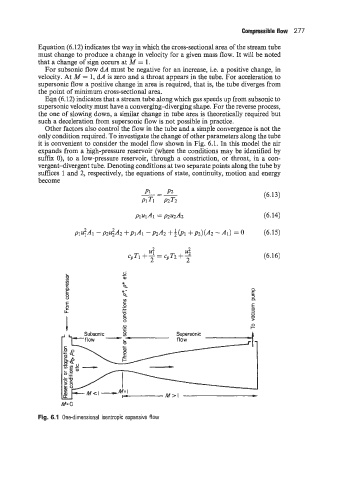
Other factors also control the flow in the tube and a simple convergence is not the
only condition required. To investigate the change of other parameters along the tube
it is convenient to consider the model flow shown in Fig. 6.1. In this model the air
expands from a high-pressure reservoir (where the conditions may be identified by
suffix 0), to a low-pressure reservoir, through a constriction, or throat, in a con-
vergent-divergent tube. Denoting conditions at two separate points along the tube by
suffices 1 and 2, respectively, the equations of state, continuity, motion and energy
become
P1 - P2 (6.13)
PlTl P2T2

(6.14)

PI441 -P2&2+P1A1 -p2A2+4(p1+p2)(A2-A1) =o (6.15)

(6.16)

s
a
n

M= 0
Fig. 6.1 One-dimensional isentropic expansive flow