Page 427 - Air pollution and greenhouse gases from basic concepts to engineering applications for air emission control

13.4 Separation of Nanoaerosol from the Air 407

where m, k and T denote particle mass, the Boltzmann constant and temperature,
respectively. Following the analysis that is similar to the molecular dynamics
introduced in Sect. 2.1, the mean impact speed of the nanoaerosol particles is
described by Eq. (13.19)

r ffiffiffiffiffiffiffiffi
8kT
v im ¼ ð13:19Þ
pm
where the mass (m) in the denominator is now the mass of a single nanoaerosol
3
particle instead of that of a gas molecule. With the mass of a particle, m = ρ p πd p /6,
Eq. (13.9) becomes
s ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
48kT
v im ¼ 2 3 ð13:20Þ
p q d
p p
Equation (13.4) shows that v im / d 1:5 . Therefore, the mean thermal impact
p
speed increase dramatically as particle size drops.
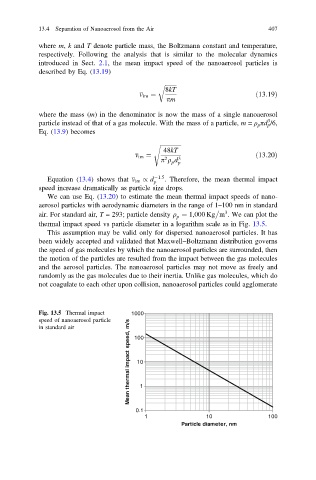
We can use Eq. (13.20) to estimate the mean thermal impact speeds of nano-
aerosol particles with aerodynamic diameters in the range of 1–100 nm in standard
3
air. For standard air, T = 293; particle density q ¼ 1,000 Kg m . We can plot the
p
thermal impact speed vs particle diameter in a logarithm scale as in Fig. 13.5.
This assumption may be valid only for dispersed nanoaerosol particles. It has
been widely accepted and validated that Maxwell–Boltzmann distribution governs
the speed of gas molecules by which the nanoaerosol particles are surrounded, then
the motion of the particles are resulted from the impact between the gas molecules
and the aerosol particles. The nanoaerosol particles may not move as freely and
randomly as the gas molecules due to their inertia. Unlike gas molecules, which do
not coagulate to each other upon collision, nanoaerosol particles could agglomerate

Fig. 13.5 Thermal impact 1000
speed of nanoaerosol particle
Mean thermal impact speed, m/s 10 1
in standard air 100

0.1
1 10 100
Particle diameter, nm